La vidéo : Inégalité de Cauchy-Schwarz
Dans cet article de “Démo sans mots“, une célèbre inégalité : l’inégalité de Cauchy-Schwarz.
Cette démonstration provient du livre Proof without words III de Roger B. Nelsen, à la page 98.
Plus de précision
Aire du parallélogramme
Dans cette vidéo, j’ai calculé l’aire du parallélogramme en utilisant une formule peu courante. Je vais détailler ci-dessous d’où elle vient.
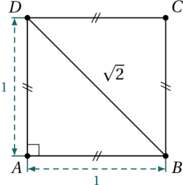
On retient habituellement que l’aire d’un parallélogramme se calcule en multipliant sa base et sa hauteur. Dans la figure ci-dessous, on trouve alors ![]() .
.
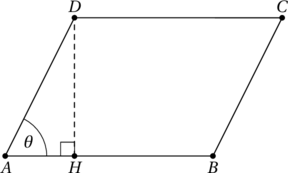
Or, en utilisant les relations CAH-SOH-TOA dans le triangle rectangle ![]() , on a que
, on a que ![]() . L’aire du parallélogramme
. L’aire du parallélogramme ![]() est donc :
est donc :
![Rendered by QuickLaTeX.com \[A_{ABCD} = \text{base} \times \text{hauteur} = AB \times DH = AB \times AD \times \sin\theta\]](https://coindesmaths.fr/wp-content/ql-cache/quicklatex.com-5b3faafdf2b2baaec3f3a28c6d4cef16_l3.png)
On peut alors calculer l’aire du parallélogramme de la vidéo, sans oublier le théorème de Pythagore pour calculer les longueurs de ses côtés.

Avec des vecteurs
Pour rappel, la vidéo démontre l’inégalité suivante :
![Rendered by QuickLaTeX.com \[|ax + by| \leqslant \sqrt{a^2 + b^2} \times \sqrt{x^2 + y^2}\]](https://coindesmaths.fr/wp-content/ql-cache/quicklatex.com-f961a949156449b7af9a1cb6f47c0acc_l3.png)
Cependant, elle se termine en mettant en avant une autre inégalité :
![Rendered by QuickLaTeX.com \[\left| \left\langle \begin{pmatrix} a \\ b \end{pmatrix} , \begin{pmatrix} x \\ y \end{pmatrix} \right\rangle \right| \leqslant \left\lVert \begin{pmatrix} a \\ b \end{pmatrix} \right\rVert \times \left\lVert \begin{pmatrix} x \\ y \end{pmatrix} \right\rVert\]](https://coindesmaths.fr/wp-content/ql-cache/quicklatex.com-ca9792ef85121b88c0c4fbfc809b95b7_l3.png)
En effet, si on note ![]() le produit scalaire des vecteurs
le produit scalaire des vecteurs ![]() et
et ![]() et
et ![]() la norme induite d’un vecteur
la norme induite d’un vecteur ![]() , leurs expressions utilisant les coordonnées des vecteurs nous redonnent la première inégalité. L’inégalité de Cauchy-Schwarz s’exprime ainsi plus simplement :
, leurs expressions utilisant les coordonnées des vecteurs nous redonnent la première inégalité. L’inégalité de Cauchy-Schwarz s’exprime ainsi plus simplement :
![Rendered by QuickLaTeX.com \[\left| \left\langle u , v \right\rangle \right| \leqslant \left\lVert u \right\rVert \left\lVert v \right\rVert\]](https://coindesmaths.fr/wp-content/ql-cache/quicklatex.com-86dfb81d2e52b15d6537c902c5cb2ff4_l3.png)
Le produit scalaire de deux vecteurs est inférieur au produit de leurs normes. C’est surtout sous cette forme que l’inégalité de Cauchy-Schwarz est connue.
Pour aller plus loin, je rajouterai que cette propriété est assez générale puisqu’elle est vraie dans les espaces préhilbertiens réels (et complexes). En particulier, elle est vraie dans ![]() , quelle que soit la dimension
, quelle que soit la dimension ![]() . La vidéo montre le cas de
. La vidéo montre le cas de ![]() .
.
Une démonstration classique mais élégante
La démonstration que je vais vous présenter maintenant est la démonstration classique de l’inégalité de Cauchy-Schwarz. Cependant, je trouve cette démonstration assez élégante, c’est pourquoi j’en parle aujourd’hui.
Pour rappel, nous allons montrer que pour deux vecteurs ![]() et
et ![]() , on a :
, on a :
![Rendered by QuickLaTeX.com \[\left| \left\langle u , v \right\rangle \right| \leqslant \left\lVert u \right\rVert \left\lVert v \right\rVert\]](https://coindesmaths.fr/wp-content/ql-cache/quicklatex.com-86dfb81d2e52b15d6537c902c5cb2ff4_l3.png)
Pour cette démonstration, il faut considérer la fonction suivante :
![Rendered by QuickLaTeX.com \[\begin{array}{r|ccc} f : & \mathbb{R} & \longrightarrow & \mathbb{R} \\ & \lambda & \longmapsto & \left\lVert u + \lambda v \right\rVert^2 \end{array}\]](https://coindesmaths.fr/wp-content/ql-cache/quicklatex.com-5cf9dd613b8ec0844fabda58a23ba661_l3.png)
Par définition, cette fonction ![]() est positive. De plus, si nous développons la norme, on a :
est positive. De plus, si nous développons la norme, on a :
![Rendered by QuickLaTeX.com \[f(\lambda) = \left\lVert u + \lambda v \right\rVert^2 = \left\lVert u \right\rVert^2 + 2 \left\langle u , v \right\rangle \lambda + \left\lVert v \right\rVert^2 \lambda^2\]](https://coindesmaths.fr/wp-content/ql-cache/quicklatex.com-a56b7c6d04954934a3a0fe95d506d896_l3.png)
Si ![]() , l’inégalité de Cauchy-Schwarz est vraie pour tout vecteur
, l’inégalité de Cauchy-Schwarz est vraie pour tout vecteur ![]() .
.
Dans le cas contraire, si ![]() , la fonction
, la fonction ![]() est un polynôme de degré 2. De plus, comme cette fonction est positive, son discriminant
est un polynôme de degré 2. De plus, comme cette fonction est positive, son discriminant ![]() est négatif. Alors :
est négatif. Alors :
![Rendered by QuickLaTeX.com \[\renewcommand*{\arraystretch}{1.5} \begin{array}{rcl} \Delta \leqslant 0 &\Rightarrow& \left(2 \left\langle u , v \right\rangle\right)^2 + 4 \times \left\lVert u \right\rVert^2 \times \left\lVert v \right\rVert^2 \leqslant 0 \\ &\Rightarrow& 4 \left\langle u , v \right\rangle^2 - 4 \left\lVert u \right\rVert^2 \left\lVert v \right\rVert^2 \leqslant 0 \\ &\Rightarrow& \left\langle u , v \right\rangle^2 \leqslant \left\lVert u \right\rVert^2 \left\lVert v \right\rVert^2 \\ &\Rightarrow& \sqrt{\left\langle u , v \right\rangle^2} \leqslant \sqrt{\left\lVert u \right\rVert^2} \sqrt{\left\lVert v \right\rVert^2} \\ &\Rightarrow& \left| \left\langle u , v \right\rangle \right| \leqslant \left\lVert u \right\rVert \left\lVert v \right\rVert \\ \end{array}\]](https://coindesmaths.fr/wp-content/ql-cache/quicklatex.com-69489a27e6c51b06026267ac6f83974c_l3.png)
Notons également que cette inégalité est une égalité si, et seulement si, ![]() . Cela est équivalent à l’existence de
. Cela est équivalent à l’existence de ![]() tel que
tel que ![]() , donc à la colinéarité des vecteurs
, donc à la colinéarité des vecteurs ![]() et
et ![]() .
.
Application géométrique
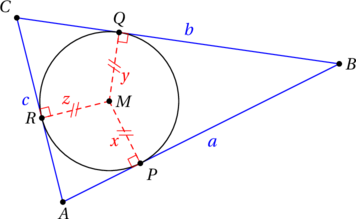
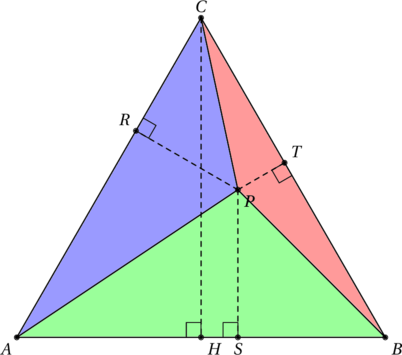
Considérons un triangle ![]() , ainsi qu’un point
, ainsi qu’un point ![]() à l’intérieur de ce triangle. Notons
à l’intérieur de ce triangle. Notons ![]() ,
, ![]() et
et ![]() les projetés orthogonaux de
les projetés orthogonaux de ![]() sur
sur ![]() ,
, ![]() et
et ![]() respectivement.
respectivement.
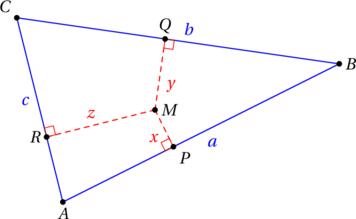
Question : Où placer le point ![]() pour que la quantité
pour que la quantité ![]() soit minimale ?
soit minimale ?
En utilisant les notations de la figure, cela signifie que l’on veut minimiser ![]() . Or, on peut écrire :
. Or, on peut écrire :
![Rendered by QuickLaTeX.com \[a = \sqrt{\frac{a}{x}} \sqrt{ax} \qquad b = \sqrt{\frac{b}{x}} \sqrt{bx} \qquad c = \sqrt{\frac{c}{x}} \sqrt{cx}\]](https://coindesmaths.fr/wp-content/ql-cache/quicklatex.com-c75b35354288835b6c6ac8077c37e20e_l3.png)
Grâce à cette forme, et en utilisant l’inégalité Cauchy-Schwarz, on a :
![Rendered by QuickLaTeX.com \[(a + b + c)^2 = \left( \sqrt{\frac{a}{x}} \sqrt{ax} + \sqrt{\frac{b}{x}} \sqrt{bx} + \sqrt{\frac{c}{x}} \sqrt{cx} \right)^2 \leqslant \left( \dfrac{a}{x} + \dfrac{b}{y} + \dfrac{c}{z} \right) \left( ax + by + cy \right)\]](https://coindesmaths.fr/wp-content/ql-cache/quicklatex.com-3c6832797e23951dbd06386f56c9e2b7_l3.png)
On reconnait l’expression à minimiser dans le membre de droite. Notons ![]() le périmètre du triangle
le périmètre du triangle ![]() et
et ![]() son aire. On a directement que
son aire. On a directement que ![]() , que l’on retrouve dans le membre de gauche.
, que l’on retrouve dans le membre de gauche.
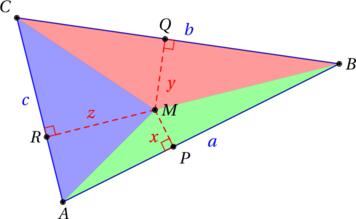
Calculons maintenant l’aire ![]() de ce triangle. Pour cela, nous allons le découper en trois triangles grâce au point
de ce triangle. Pour cela, nous allons le découper en trois triangles grâce au point ![]() , comme représenté ci-dessus. Ainsi, l’aire de
, comme représenté ci-dessus. Ainsi, l’aire de ![]() est égale à la somme de celles des triangles
est égale à la somme de celles des triangles ![]() ,
, ![]() ,
, ![]() .
.
![Rendered by QuickLaTeX.com \[\mathcal{A} = \mathcal{A}_{AMB} + \mathcal{A}_{BMC} + \mathcal{A}_{CMA} = \frac{ax}{2} + \frac{by}{2} + \frac{cz}{2} = \frac{1}{2} (ax + by + cz)\]](https://coindesmaths.fr/wp-content/ql-cache/quicklatex.com-dd288c3931e926b0ef1159ad164a9a95_l3.png)
On trouve ainsi que ![]() . Finalement, en utilisant les expressons de
. Finalement, en utilisant les expressons de ![]() et
et ![]() que nous venons d’établir, on a :
que nous venons d’établir, on a :
![Rendered by QuickLaTeX.com \[\mathcal{P}^2 \leqslant \left( \dfrac{a}{x} + \dfrac{b}{y} + \dfrac{c}{z} \right) \times 2\mathcal{A} \qquad \Longleftrightarrow \qquad \frac{\mathcal{P}^2}{2\mathcal{A}} \leqslant \dfrac{a}{x} + \dfrac{b}{y} + \dfrac{c}{z}\]](https://coindesmaths.fr/wp-content/ql-cache/quicklatex.com-fdad1e17a135143a17749e3a0607f02f_l3.png)
Nous voilà donc avec une minoration de la quantité ![]() . Mais n’oublions le cas d’égalité de l’inégalité de Cauchy-Schwarz : cette inégalité est une égalité si, et seulement si, les vecteurs
. Mais n’oublions le cas d’égalité de l’inégalité de Cauchy-Schwarz : cette inégalité est une égalité si, et seulement si, les vecteurs ![]() et
et ![]() sont colinéaires. Cela est équivalent à l’existence d’un
sont colinéaires. Cela est équivalent à l’existence d’un ![]() tel que :
tel que :
![Rendered by QuickLaTeX.com \[\renewcommand*{\arraystretch}{1.5} \left\lbrace\begin{array}{rcl} \sqrt{\frac{a}{x}} &=& \lambda \sqrt{ax} \\ \sqrt{\frac{b}{y}} &=& \lambda \sqrt{by} \\ \sqrt{\frac{c}{z}} &=& \lambda \sqrt{cz} \end{array}\right. \quad\Longleftrightarrow\quad \left\lbrace\begin{array}{rcl} \sqrt{a} &=& \lambda \sqrt{a}x \\ \sqrt{b} &=& \lambda \sqrt{b}y \\ \sqrt{c} &=& \lambda \sqrt{c}z \end{array}\right. \quad\Longleftrightarrow\quad \left\lbrace\begin{array}{rcl} \frac{1}{\lambda} &=& x \\ \frac{1}{\lambda} &=& y \\ \frac{1}{\lambda} &=& z \end{array}\right.\]](https://coindesmaths.fr/wp-content/ql-cache/quicklatex.com-a209c153f19cfe54118bb4ea7ed0c48d_l3.png)
On a ainsi l’égalité si, et seulement si, ![]() . Autrement dit, la quantité
. Autrement dit, la quantité ![]() est minimale lorsque le point
est minimale lorsque le point ![]() est à la même distance des trois côtés du triangle, c’est-à-dire lorsque
est à la même distance des trois côtés du triangle, c’est-à-dire lorsque ![]() est le centre du cercle inscrit au triangle
est le centre du cercle inscrit au triangle ![]() .
.

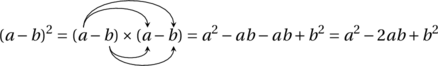
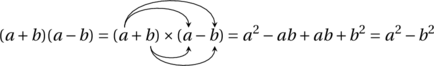


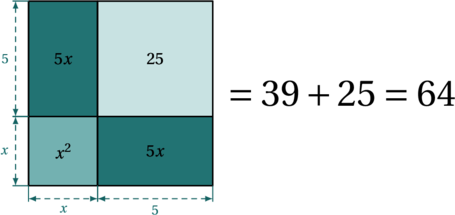
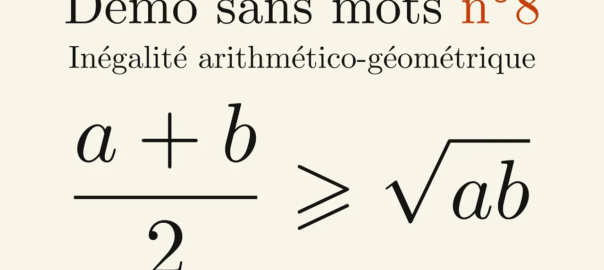

![Rendered by QuickLaTeX.com \[A = ab \leqslant \left( \frac{a + b}{2} \right)^2 = \left( \frac{\frac{P}{2}}{2} \right)^2 = \left( \frac{P}{4} \right)^2 = \frac{P^2}{16}\]](https://coindesmaths.fr/wp-content/ql-cache/quicklatex.com-4746efbfe56b372c4edcf7b0859cd42b_l3.png)
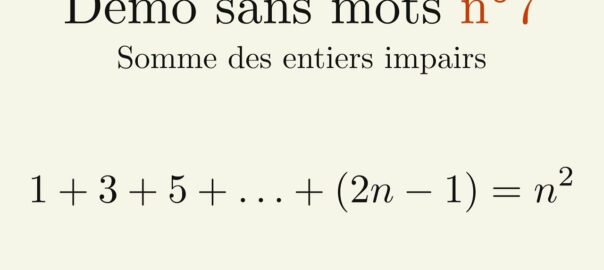
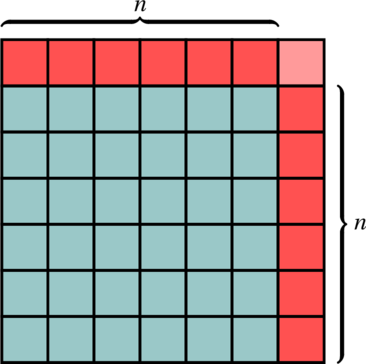
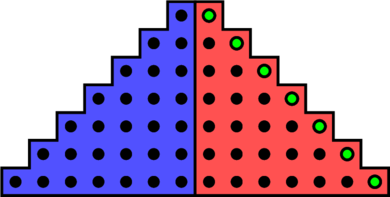









![Rendered by QuickLaTeX.com \begin{equation*} \footnotesize \setlength{\arraycolsep}{2.5pt} \begin{array}{*{16}{c}} S &=& \textcolor{teal}{1} &+& \textcolor{olive}{2} &+& \textcolor{purple}{3} &+& \ldots &+& \textcolor{purple}{(n-2)} &+& \textcolor{olive}{(n-1)} &+& \textcolor{teal}{n} \\ S &=& \textcolor{teal}{n} &+& \textcolor{olive}{(n-1)} &+& \textcolor{purple}{(n-2)} &+& \ldots &+& \textcolor{purple}{3} &+& \textcolor{olive}{2} &+& \textcolor{teal}{1} \\\hline 2S &=& \textcolor{teal}{(n+1)} &+& \textcolor{olive}{(n+1)} &+& \textcolor{purple}{(n+1)} &+& \ldots &+& \textcolor{purple}{(n+1)} &+& \textcolor{olive}{(n+1)} &+& \textcolor{teal}{(n+1)} \\ \multicolumn{2}{c}{} & \multicolumn{14}{c}{\raisebox{.5\normalbaselineskip}[0pt][0pt]{$\underbrace{\hspace*{31.2em}}$}} \\ \multicolumn{2}{c}{} & \multicolumn{14}{c}{n \text{ fois}} \\ \end{array} \end{equation*}](https://coindesmaths.fr/wp-content/ql-cache/quicklatex.com-fd55e31c58af544a312c766cd742b2ac_l3.png)