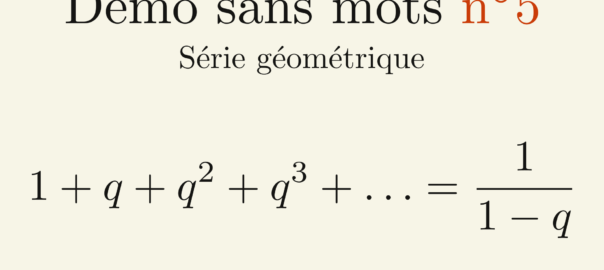La vidéo : Série géométrique

Dans ce volet de « Démo Sans Mots« , nous parlerons de série géométrique. Cet article sera plus technique que les précédents.

Cette démonstration de Benjamin Klein et Irl Bivens a été publiée dans le Mathematics Magazine, (Vol. 61, No. 4, p. 219) en octobre 1988.

Somme de termes d’une suite géométrique

Avant d’attaquer pleinement le sujet, penchons-nous d’abord sur quelques préliminaires.

Pour ceux qui ne le savent pas, le mot « géométrique » utilisé ici ne veut pas dire que l’on utilise des cercles ou des rectangles. Il veut plutôt dire qu’on utilise des nombres obtenus les uns après les autres en multipliant par un même nombre , appelée raison. Cette suite de nombres est ainsi appelée suite géométrique.

Ce que l’on fait dans cette vidéo, c’est calculer la somme de tous ses nombres, jusqu’à l’infini. Mais commençons doucement en en prenant qu’un nombre fini. Disons . Et notons la somme de ces termes.

Écrivons maintenant cette addition en entier, puis écrivons cette même addition en multipliant tous ses termes par .

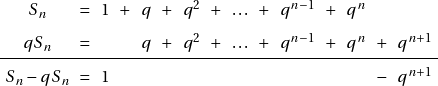
Ce jeu d’écriture nous permet de facilement calculer comme ci-dessus. On obtient ainsi que , c’est-à-dire que .

Des arguments sous-entendus

Nous avons maintenant tous les outils nécessaires pour justifier rigoureusement certains arguments qui sont sous-entendus dans cette démonstration visuelle : la convergence de la série, l’alignement des points et l’origine de la formule.

Convergence de la série

Avant de chercher à calculer notre somme, il faut d’abord savoir si elle existe. En effet, il n’est pas évident que la somme d’une infinité de termes soit un nombre fini, et ce n’est d’ailleurs pas le cas en général.

En fait, dans notre cas, il nous suffit de partir du cas vu dans la partie précédente avec un nombre fini de termes, puis de regarder ce qui se passe en en prenant de plus en plus. Dans notre cas, puisque , on a que tend vers 0, donc la suite des est bien convergente de limite

Nous venons ainsi de démontrer notre résultat, mais il nous reste encore un peu de travail pour justifier la démonstration visuelle. Nous noterons cette limite dans la suite. On parle de plus de série géométrique.

Alignement des points

Pour ce deuxième point, nous allons avoir besoin de nommer les points de la figure. Je vous propose les notations ci-dessous.

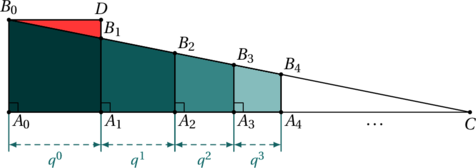
Notre objectif est de montrer que les points , , , , … sont alignés. Plus exactement, nous allons montrer que pour n’importe quelle valeur d’un entier , les points , et sont alignés. Pour cela, nous allons montrer que les triangles et sont semblables.

Commençons par un calcul intermédiaire, avec la longueur .

Nous pouvons maintenant montrer que les rapports et sont égaux.

Finalement, on a et les triangles et sont rectangles respectivement en et en . Ces triangles sont donc semblables, donc les angles et sont égaux, et les points , et sont alignés.

Origine de la formule

La seule chose qu’il nous reste à faire, c’est d’expliquer d’où vient la formule maintenant qu’on a la figure. Et il suffit de remarquer que les triangles et sont semblables. Ils ont donc des côtés qui ont des longueurs proportionnelles.