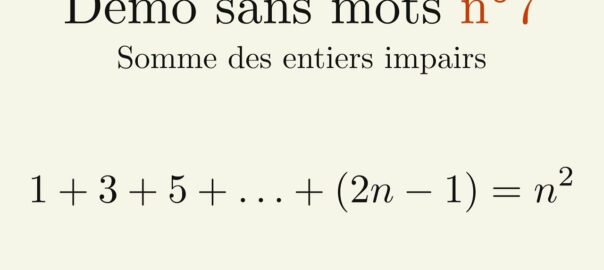Miniature de la vidéo numéro 7 de la série Démo Sans Mots, qui porte sur la somme des entiers impairs de 1 à 2n-1.

Somme des entiers impairs – DSM#7

Mathématiques, Vidéos, ,

La vidéo : Somme des entiers impairs

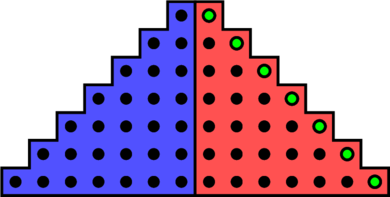
Pour ce septième épisode de “Démo sans mots“, je vous propose une démonstration similaire à celle du premier épisode. En effet, nous allons parler de la somme des entiers impairs de 1 à n.

Cette démonstration provient du livre Proof without words de Roger B. Nelsen, à la page 71.

Comme dans le premier épisode, la démonstration présentée dans la vidéo n’est qu’un exemple, celle du cas n=6. Mais les autres cas fonctionnent de la même manière.

EDIT : Plus de rigueur

Suite à un commentaire sous la vidéo, je vais développer avec rigueur la démonstration qui y est présentée.

Cette démonstration est en fait une démonstration par récurrence, où chaque nombre impair est ajouté un à un. Nous allons donc démontrer que P(n) : 1 + 3 + 5 + \ldots + (2n - 1) = n^2 est vraie pour tout entier n supérieur ou égal à 1.

Initialisation : P(1) : 1 = 1^2, je pense que cela se passe de justification.

Hérédité : Supposons que P(n) est vrai, c’est-à-dire que 1 + 3 + 5 + \ldots + (2n - 1) = n^2. L’objectif est de montrer P(n+1) : 1 + 3 + 5 + \ldots + (2n + 1) = (n +1)^2.

En utilisant l’identité remarquable (a + b)^2 = a^2 + 2ab + b^2, ce résultat se trouve facilement :

      \[1 + 3 + 5 + \ldots + (2n - 1) + (2n + 1) = n^2 + (2n + 1) = (n + 1)^2\]

Visuellement, cela se représente par la colonne qui se “replie” sur le carré précédent. Il y a alors n cases à droite du carré, n cases au-dessus du carré, et une dernière case dans l’angle, soit un total de 2n+1 cases pour former un carré plus grand.

Rendered by QuickLaTeX.com

Conclusion : Pour tout n supérieur ou égal à 1, on a 1 + 3 + 5 + \ldots + (2n - 1) = n^2.

En partant de ce que l’on sait

Dans le premier épisode, nous avons démontré le résultat suivant :

      \[1 + 2 + 3 + \ldots + n = \frac{n(n+1)}{2}\]

Nous pouvons utiliser cette première égalité afin de démontrer notre nouvelle formule d’une manière différente de celle de la vidéo.

En effet, commençons par réécrire notre somme. Pour cela, nous allons écrire chaque nombre impair sous la forme 2k-1, avec k un entier. Voici ce qu’on obtient :

      \[1 + 3 + 5 + \ldots + (2n - 1)= (2 \times 1 - 1) + (2 \times 2 - 1) + (2 \times 3 - 1) + \ldots + (2 \times n - 1)\]

Cette somme, peu évidente au premier abord, sera plus simple à calculer en réorganisant ses termes. Nous allons regrouper les termes de la forme 2k d’un côté et les -1 de l’autre.

      \[1 + 3 + 5 + \ldots + (2n - 1)= (2 \times 1 + 2 \times 2 + 2 \times 3 + \ldots + 2 \times n) + n \times (-1)\]

Désormais, nous pouvons non seulement factoriser la première parenthèse par 2, mais également calculer le dernier terme.

      \[1 + 3 + 5 + \ldots + (2n - 1)= 2 \times (1 + 3 + 5 + \ldots + n) - n\]

On retrouve finalement la somme des n premiers entiers, que nous pouvons remplacer par notre égalité déjà démontrée.

      \[2 \times (1 + 3 + 5 + \ldots + n) - n = 2 \times \frac{n(n+1)}{2} - n = n (n + 1) - n = n^2 + n - n = n^2\]

On a donc bien retrouvé le résultat de la vidéo. Notons que cette dernière égalité peut elle aussi se retrouver visuellement.

Rendered by QuickLaTeX.com

Galilée et la chute des corps

Dans l’Italie de la Renaissance, Galilée, célèbre physicien, astronome et mathématicien, s’intéresse à la chute des corps. En 1638, il publie son dernier ouvrage, intitulé Discours et démonstrations mathématiques concernant deux sciences nouvelles. Ce livre, véritable testament scientifique, regroupe les fruits de trois décennies de recherches en physique.

Dans ce livre, Galilée expose sa conviction : la chute des corps se fait selon un mouvement uniformément accéléré. C’est-à-dire que la vitesse augmente de manière proportionnelle au temps. C’est la première fois que ce type de mouvement est décrit aussi rigoureusement.

Plan incliné exposé au Musée Galilée (Florence) et construit au XIXe siècle. Même si aucun document ne l’atteste, Galilée aurait pu utiliser un outil similaire.
Plan incliné exposé au Musée Galilée (Florence) et construit au XIXe siècle. Même si aucun document ne l’atteste, Galilée aurait pu utiliser un outil similaire.

Ces définitions mathématiques permettent alors à Galilée de démontrer les propriétés du mouvement dans ce qu’on appellera plus tard la mécanique classique. Il en ressort une propriété qui nous rapproche de notre sujet du jour.

Les distances parcourues, pendant des intervalles de temps égaux, par un corps tombant à partir du repos, sont les unes par rapport aux autres dans le même rapport que les nombres impairs, en commençant par l’unité.

Galilée, Discours et démonstrations mathématiques concernant deux sciences nouvelles [190], 1638

Reformulons. Imaginons un objet qui tombe, quel qu’il soit. Lors de la première seconde, cet objet parcourt une certaine distance. Par la suite, il parcourra trois fois cette distance pendant la deuxième seconde, puis cinq fois cette distance pendant la troisième seconde, et ainsi de suite. En notant d la distance parcourue la première seconde, les distances suivantes sont donc 3 \times d, 5 \times d, 7 \times d, etc… On retrouve notre somme des entiers impairs.

Ainsi, si nous cherchons à calculer la distance totale parcourue, il faut additionner toutes ces distances. Au bout de n secondes, notre objet aura parcouru une distance égale à :

      \[d + 3 \times d + 5 \times d + \ldots + (2n+1) \times d=d \times (1 + 3 + 5 + \ldots + (2n-1))=d \times n^2\]

On peut en conclure, comme Galilée, que la distance parcourue en chute libre est proportionnelle au carré de la durée du trajet.

Pour plus de détails, je vous renvoie vers cet article publié sur Zeste de savoir.

Laisser un commentaire

Votre adresse e-mail ne sera pas publiée. Les champs obligatoires sont indiqués avec *

seize + sept =