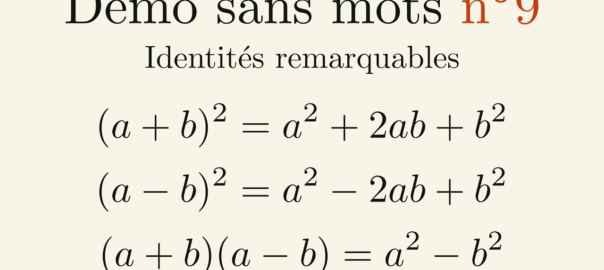La vidéo : Identités remarquables
Cette fois dans “Démo sans mots“, un incontournable pour tous les collégiens et lycéens : les identités remarquables.
La démonstration de la première identité remarquable provient des Éléments d’Euclide (Livre II, Proposition 4). Je n’ai pas trouvé d’origine pour les deux autres
Démonstrations algébriques
L’égalité 
était en réalité déjà connue par les Babyloniens. Euclide la démontre dans le livre II de ses Éléments et la formule ainsi :
Si un segment de droite est divisé en deux parties, le carré du segment entier est égal aux carrés des deux parties plus deux fois le rectangle contenu par les deux parties.
Euclide, Les Éléments, Livre II, Proposition 4
Je vous l’assure, il s’agit bien de la même chose. Rappelons qu’à cette époque, le raisonnement reposait avant tout sur l’utilisation de représentations géométriques, même pour les calculs.
Même si aujourd’hui ces démonstrations utilisant la géométrie sont toujours parfaitement correctes, nous avons plutôt tendance à passer par le calcul. C’est peut-être comme ça que vous les avez découvertes la première fois, et c’est également ce que nous allons voir ci-dessous.
À l’instar de la démonstration d’Euclide, nous avons besoin de savoir développer. Si dans les Éléments, on trouve la démonstration de trois premières égalités (dans l’ordre
![\[a (b_1 + b_2 + \ldot + b_n) = a b_1 + a b_2 + \ldots + a b_n,\]](https://coindesmaths.fr/wp-content/ql-cache/quicklatex.com-a6c73f73afa4183c8e36588772313190_l3.png "Rendered by QuickLaTeX.com")
![\[(a+b)^2 = (a + b) \times a + (a + b) \times b,\]](https://coindesmaths.fr/wp-content/ql-cache/quicklatex.com-f8290e5290785f6aa764060f5ae1ec0d_l3.png "Rendered by QuickLaTeX.com")
![\[\text{et}\quad(a + b) \times a = a^2 + ab\]](https://coindesmaths.fr/wp-content/ql-cache/quicklatex.com-31645ab10169cbcdef86971aae0c4471_l3.png "Rendered by QuickLaTeX.com")
toujours d’un point de vue géométrique), nous allons développer selon l’égalité suivante :
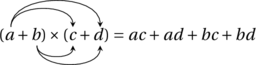
Allons-y ! Lançons-nous dans les calculs !
Et de une…
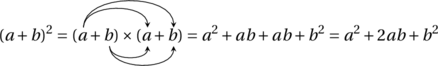
… et de deux…
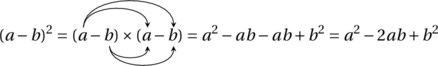
… et de trois !
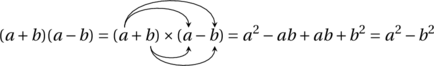
Nous avons donc bien retrouvé nos trois identités remarquables.
Compléter le carré
Bagdad, début du IXe siècle. Le Calife abbasside Al-Ma’mūn sollicite Al-Khwarizmi, savant renommé, afin de créer une synthèse des méthodes mathématiques nécessaires pour administrer son vaste empire.
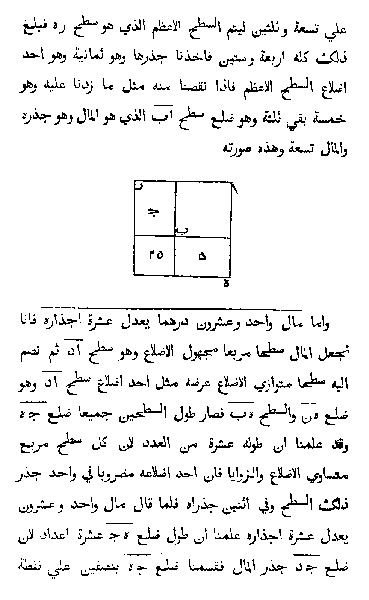
L’un des problèmes résolus par Al-Khwarizmi est le suivant :
Un bien et dix de ses racines égalent trente-neuf dirhams.
Al-Kwarizmi, Abrégé du calcul par la restauration et la comparaison
Ce qui donne avec le symbolisme d’aujourd’hui : 
.
La méthode de résolution, telle qu’elle a été écrite par Al-Khwarizmi, est la suivante :
Son procédé de résolution consiste à diviser les racines par deux, et c’est cinq dans ce problème. Tu le multiplies par lui-même et ce sera vingt-cinq. Tu l’ajoutes à trente-neuf. Cela donnera soixante-quatre. Tu prends alors sa racine carrée qui est huit et tu en retranches la moitié du nombre des racines et c’est cinq. Il reste trois et c’est la racine du bien que tu cherches et le bien est neuf.
Al-Kwarizmi, Abrégé du calcul par la restauration et la comparaison
Cette méthodologie peut sembler obscure, mais le raisonnement est géométrique, comme nous allons le voir.
En effet, si le terme 
se représente par un carré de côté 
, le terme 
se représentent par deux rectangles de longueur 
et collés au carré, comme représenté ci-dessous :
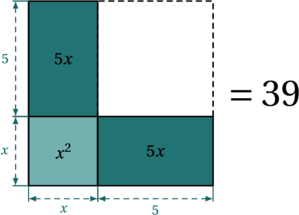
L’aire colorée est donc égale à 
, comme le premier membre de l’équation. L’idée est de compléter le carré, afin de calculer facilement la racine.
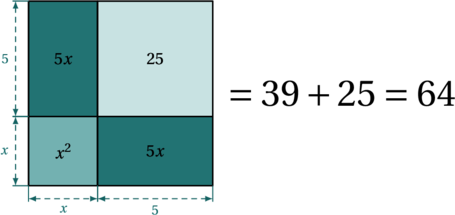
On se retrouve ainsi avec un carré de côté 
, dont l’aire est égale à 
, soit 
. Al-Khwarizmi en déduit alors que 
, donc que 
. Et en effet, est bien solution de cette équation, puisque 
.
N’oublions pas qu’aujourd’hui il faudrait rajouter une autre solution : 
. Cela vient du fait que 
vaut également . Mais à l’époque d’Al-Khwarizmi comme celle d’Euclide, les raisonnements étant géométrique, et les nombres étant des longueurs, les nombres négatifs étaient inenvisageables.