La vidéo : Encadrement de π
Pour cet épisode de « Démo Sans Mots« , nous allons nous pencher sur un nombre aussi connu que mystérieux : trouvons un encadrement de π.
Cette démonstration est inspirée des travaux d’Archimède, datant d’environ 250 avant J.-C.
Avec plus de côtés
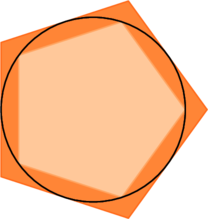
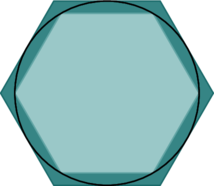
Pour trouver cet encadrement de 
, nous avons utilisé un hexagone inscrit et un carré circonscrit. Pour plus de précision, on peut tout simplement utiliser des polygones réguliers avec plus de côtés. C’est ce que nous allons détailler.
Calculons les longueurs des côtés de ses polygones. Nous allons juste avoir besoin d’un peu de trigonométrie dans les triangles rectangles. Pour rappel, nous avons les relations CAH-SOH-TOA :
![\[\footnotesize\cos(\text{angle}) = \frac{\text{adjacent}}{\text{hypoténuse}}\qquad\sin(\text{angle}) = \frac{\text{opposé}}{\text{hypoténuse}}\qquad\tan(\text{angle}) = \frac{\text{opposé}}{\text{adjacent}}\]](https://coindesmaths.fr/wp-content/ql-cache/quicklatex.com-9125738cae82b2b79cfabead9a6743a0_l3.png "Rendered by QuickLaTeX.com")
En réalité, nous n’aurons besoin que des deux dernières relations. Cela nous permet de calculer la moitié d’un coté de nos polygones, comme illustré ci-dessous. Ici, nous utiliserons des polygones ayant 
côtés.
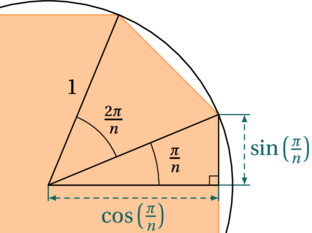
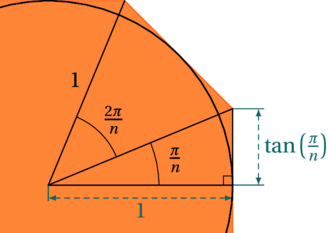
On peut ainsi calculer le périmètre des deux polygones en multipliant ces longueurs par 
. Le périmètre du polygone inscrit est donc de 
et celui du polygone circonscrit est de 
. Il ne nous reste plus qu’à encadrer le périmètre du cercle par ces deux valeurs.
![\[2n\sin\left(\frac{\pi}{n}\right) < 2\pi < 2n\tan\left(\frac{\pi}{n}\right)\qquad\Leftrightarrow\qquad n\sin\left(\frac{\pi}{n}\right) < \pi < n\tan\left(\frac{\pi}{n}\right)\]](https://coindesmaths.fr/wp-content/ql-cache/quicklatex.com-a1c2a0992b640054a2ba2bb113d8b922_l3.png "Rendered by QuickLaTeX.com")
Choisissez la valeur de que vous voulez et vous aurez donc un encadrement de . On peut même constater en plaçant ces encadrements dans un repère qu’ils deviennent de plus en plus précis. Cette méthode permet ainsi de trouver des approximations de pour de grandes valeurs de .
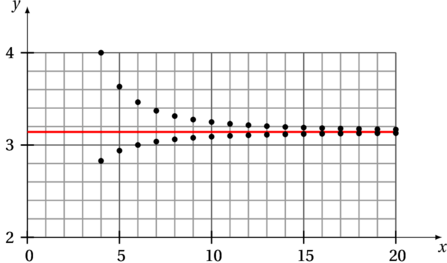
Cette méthode fut plus ou moins celle utilisée par Archimède. Il a réussi, grâce à un polygone à 96 côtés, à déterminer que 
.
Méthode de Monté-Carlo
D’autres méthodes classiques permettant de trouver des approximations de sont celle de Monté-Carlo. Ces méthodes tiennent leur nom du quartier de Monaco où se trouve un célèbre casino. Et pourquoi ça ? Eh bien parce que ces méthodes reposent sur des tirages aléatoires.
En effet, on peut partir par example d’un cercle de rayon 1 inscrit dans un carré. Si on choisit au hasard un point dans ce carré, quelle serait la probabilité 
qu’il soit dans le cercle ? En raisonnant avec les aires, voici ce qu’on obtient :
![\[P= \frac{\text{Aire}(\text{cercle})}{\text{Aire}(\text{carré})}= \frac{\pi \times 1^2}{2^2}= \frac{\pi}{4}\]](https://coindesmaths.fr/wp-content/ql-cache/quicklatex.com-f5fe879b1083f495f138afd141a27bc3_l3.png "Rendered by QuickLaTeX.com")
Ainsi, si nous faisons un grand nombre de tirages, le quotient du nombre de points dans le cercle par rapport au nombre de points au total devrait se rapprocher de 
. En multipliant cette valeur par 4, nous aurons une approximation de .
Lançons maintenant cette simulation numérique.
Et nous obtenons bien une approximation de !
Notons cependant que les méthodes que nous venons de voir ont besoin de beaucoup d’étapes avant de nous donner quelques décimales. Beaucoup d’autres méthodes existent aujourd’hui, et peuvent nous donner plusieurs décimales et quelques étapes, mais ce sera pour de prochaines fois…