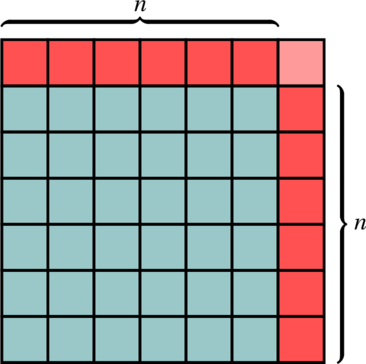
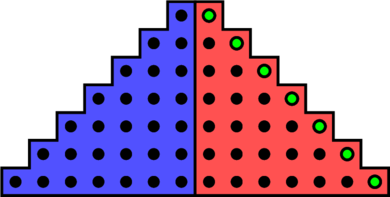
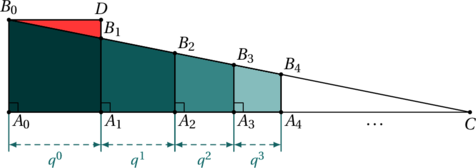
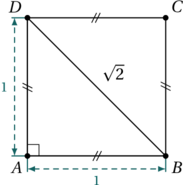
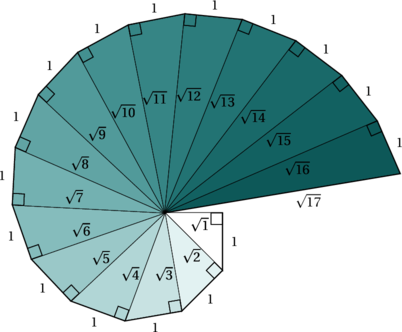
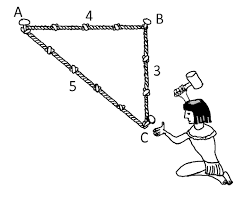
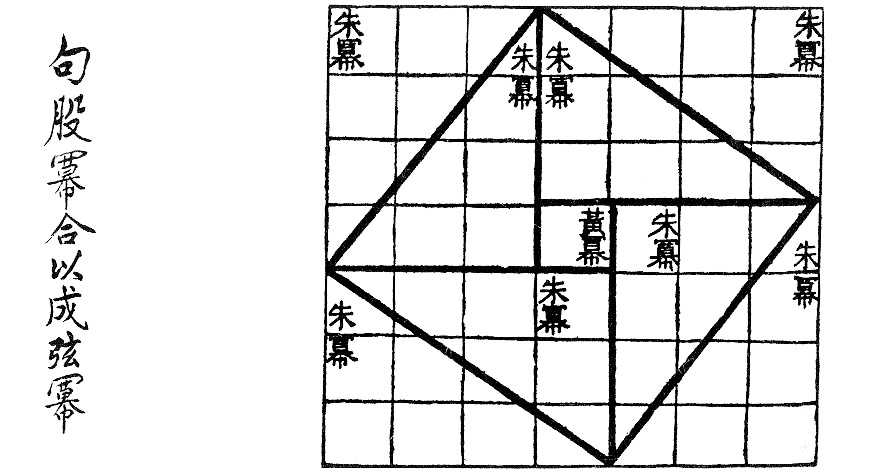
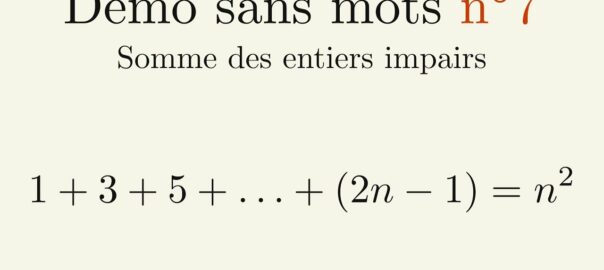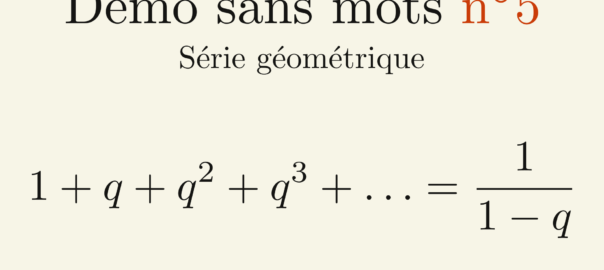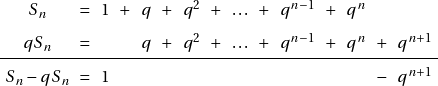Les nombres complexes sont apparus afins de résoudre certains problèmes. Dans cet article, nous allons voir en détail l’histoire de leur apparition.
Premiers ensembles de nombres
Le premier ensemble de nombres découvert est l’ensemble ![]() des entiers naturels, celui qui nous sert à compter. Or, cet ensemble ne permet pas de résoudre tous les problèmes qu’il nous permet d’écrire. En effet l’équation
des entiers naturels, celui qui nous sert à compter. Or, cet ensemble ne permet pas de résoudre tous les problèmes qu’il nous permet d’écrire. En effet l’équation ![]() n’admet pas de solution dans
n’admet pas de solution dans ![]() .
.
Il a donc fallu créer un ensemble plus grand, permettant de résoudre l’équation précédente, mais contenant l’ensemble ![]() . Cet ensemble est l’ensemble des entiers relatifs
. Cet ensemble est l’ensemble des entiers relatifs ![]() , qui ajoute les entiers négatifs.
, qui ajoute les entiers négatifs.
Cependant, on peut toujours trouver des équations dont les solutions ne sont pas dans ![]() . Par exemple l’équation
. Par exemple l’équation ![]() n’admet pas de solution dans
n’admet pas de solution dans ![]() . Par un procédé analogue, on a ainsi créé les ensembles
. Par un procédé analogue, on a ainsi créé les ensembles ![]() ,
, ![]() puis
puis ![]() .
.
Résolution des équations du troisième degré
Au XVIe siècle, le problème de la résolution des équations du troisième degré passionne un bon nombre de mathématiciens italiens.
Scipione Del Ferro (1465-1526) est le premier à trouver une méthode pour résoudre certaines de ces équations, mais la garde secrète. À sa mort, en 1526, son élève Anto Maria Del Fiore parvient à récupérer cette méthode. Lui aussi la garde secrète, mais décide de défier les autres mathématiciens sur la résolution de ces équations.
En 1535, Tartaglia (1499-1557) relève le défi, et s’engage dans un duel. Chacun déposa une liste de 30 problèmes chez un notaire ainsi qu’une somme d’argent. Celui qui, dans les 40 jours, aurait résolu le plus de problèmes serait désigné vainqueur et remporterait la somme.
Juste avant la date limite, Tartaglia trouve la résolution générale de ce type d’équations, et les résout toutes en quelques heures. Il remporte alors le concours mais refuse le prix. Trop heureux de sa méthode, il décide de ne pas la divulguer afin de gagner facilement d’autres concours.
Le mathématicien renommé Jérôme Cardan (1501-1576) entend parler de la réussite de Tartaglia et, après plusieurs entretiens, réussit à lui arracher sa méthode. Cardan promet de ne jamais la divulguer. Il la publie sous son nom dans son ouvrage Ars Magna un an plus tard, ayant appris entre temps que cette méthode avait été découverte par Del Ferro avant Tartaglia.
Pour l’équation ![]() , la méthode trouvée par Cardan donne la solution suivante :
, la méthode trouvée par Cardan donne la solution suivante :
![Rendered by QuickLaTeX.com \[x_0 = \sqrt[\leftroot{-1}\uproot{2}\scriptstyle 3]{\frac{q}{2} - \sqrt{\Delta}} + \sqrt[\leftroot{-1}\uproot{2}\scriptstyle 3]{\frac{q}{2} + \sqrt{\Delta}} \quad\text{si}\quad \Delta = \frac{q^2}{4} + \frac{p^3}{27} \geqslant 0\]](https://coindesmaths.fr/wp-content/ql-cache/quicklatex.com-e1b7c724a3e8e8ac92e62ff3abc7d5fe_l3.png)
Cette formule est depuis lors appelée formule de Cardan.
Un premier exemple
On considère l’équation ![]() . Nous pouvons appliquer la formule de Cardan avec
. Nous pouvons appliquer la formule de Cardan avec ![]() et
et ![]() car :
car :
![Rendered by QuickLaTeX.com \[\Delta = \frac{2^2}{4} + \frac{(-3)^3}{27} = \frac{4}{4} + \frac{-27}{27} = 1 - 1 = 0 \geqslant 0\]](https://coindesmaths.fr/wp-content/ql-cache/quicklatex.com-f557e29842319485f14d2b8b4509ab9d_l3.png)
Voici ce que l’on obtient :
![Rendered by QuickLaTeX.com \[x_0 = \sqrt[\leftroot{-1}\uproot{2}\scriptstyle 3]{\frac{2}{2} - \sqrt{0}}+\sqrt[\leftroot{-1}\uproot{2}\scriptstyle 3]{\frac{2}{2} + \sqrt{0}} = \sqrt[\leftroot{-1}\uproot{2}\scriptstyle 3]{1}+\sqrt[\leftroot{-1}\uproot{2}\scriptstyle 3]{1} = 1+1 = 2\]](https://coindesmaths.fr/wp-content/ql-cache/quicklatex.com-7c8963e8fe509a7bd6a68931f32c2f53_l3.png)
Ainsi, ![]() est solution de l’équation. En effet,
est solution de l’équation. En effet, ![]() .
.
Limites de cette formule
Considèrons maintenant l’équation ![]() . Celle-ci revient à prendre
. Celle-ci revient à prendre ![]() et
et ![]() . Voici ce qu’on obtient :
. Voici ce qu’on obtient :
![Rendered by QuickLaTeX.com \[\Delta = \frac{4^2}{4} + \frac{(-15)^3}{27} = \frac{16}{4} + \frac{-3375}{27} = 4 - 125 = -121 < 0\]](https://coindesmaths.fr/wp-content/ql-cache/quicklatex.com-ece3e426e5970079078762473cd421e1_l3.png)
Cette valeur de ![]() ne nous permet pas d’appliquer la formule de Cardan, puisqu’il faudrait calculer la racine carrée d’un nombre négatif.
ne nous permet pas d’appliquer la formule de Cardan, puisqu’il faudrait calculer la racine carrée d’un nombre négatif.
Vers la notation 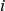 et les nombres complexes
et les nombres complexes
Au lieu de se démener, Cardan, bientôt suivi de Raphaël Bombelli (1526-1572), introduit un nombre imaginaire dont le carré vaut -1, et le note ![]() , afin de pallier ce problème.
, afin de pallier ce problème.
Une première notation et calculs intermédiaires
Avant de continuer, nous allons faire deux calculs dont nous auront besoin pour la suite.
En admettant comme eux que ![]() , et en utilisant les règles habituelles d’addition et de multiplication ainsi que le binôme de Newton, on peut obtenir les résultats suivants :
, et en utilisant les règles habituelles d’addition et de multiplication ainsi que le binôme de Newton, on peut obtenir les résultats suivants :
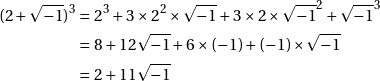
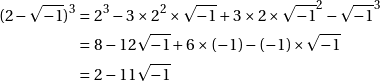
Retour à notre deuxième exemple
Reprenons l’équation ![]() . Essayons d’appliquer la formule de Cardan :
. Essayons d’appliquer la formule de Cardan :
![Rendered by QuickLaTeX.com \[x_0 = \sqrt[\leftroot{-1}\uproot{2}\scriptstyle 3]{\frac{4}{2} - \sqrt{-121}} + \sqrt[\leftroot{-1}\uproot{2}\scriptstyle 3]{\frac{4}{2} + \sqrt{-121}} = \sqrt[\leftroot{-1}\uproot{2}\scriptstyle 3]{2 - 11 \sqrt{-1}} + \sqrt[\leftroot{-1}\uproot{2}\scriptstyle 3]{2 + 11 \sqrt{-1}}\]](https://coindesmaths.fr/wp-content/ql-cache/quicklatex.com-2fb958ee3699fca741409bf4480ddb60_l3.png)
On retrouve ainsi sous les racines cubiques les membres de droites de nos calculs intermédiaires. Nous n’avons plus qu’à les utiliser :
![Rendered by QuickLaTeX.com \[x_0 = \sqrt[\leftroot{-1}\uproot{2}\scriptstyle 3]{\left( 2 - \sqrt{-1} \right)^3} + \sqrt[\leftroot{-1}\uproot{2}\scriptstyle 3]{\left( 2 + \sqrt{-1} \right)^3} = \left( 2 - \sqrt{-1} \right) + \left( 2 + \sqrt{-1} \right) = 4\]](https://coindesmaths.fr/wp-content/ql-cache/quicklatex.com-e78da440f47c3b0bba2f712b50cc40b0_l3.png)
Finalement, les nombres imaginaires que nous avons introduits s’annulent, ne laissant que ![]() comme solution. En effet,
comme solution. En effet, ![]() .
.
Le nombre complexe 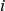
En 1774, Leonhard Euler (1707-1783) constate que cette notation ![]() contredit la règle de calcul
contredit la règle de calcul ![]() . En effet, voici le type de calcul que l’on pourrait faire avec cette notation :
. En effet, voici le type de calcul que l’on pourrait faire avec cette notation :
![Rendered by QuickLaTeX.com \[1 = \sqrt{1} = \sqrt{(-1) \times (-1)} = \sqrt{-1} \times \sqrt{-1} = -1\]](https://coindesmaths.fr/wp-content/ql-cache/quicklatex.com-7c75a362df833402a27b112b539195a3_l3.png)
Bien sûr, cette contradiction rend l’utilisation de cette notation peu pratique. Euler propose alors de remplacer la notation ![]() par la notation
par la notation ![]() . On a donc
. On a donc ![]() . La notation
. La notation ![]() sera ensuite abandonnée par souci de clarté.
sera ensuite abandonnée par souci de clarté.
Nombres complexes
Le nombre ![]() permet d’écrire des nombres de la forme
permet d’écrire des nombres de la forme ![]() , avec
, avec ![]() et
et ![]() des réels, comme
des réels, comme ![]() par exemple. Ces nombres étant composés de deux parties, ils seront appelés des nombres complexes par Carl Friedrich Gauss (1777-1855) en 1831.
par exemple. Ces nombres étant composés de deux parties, ils seront appelés des nombres complexes par Carl Friedrich Gauss (1777-1855) en 1831.
Ainsi, nous avons pu voir que les nombres complexes permettent de trouver des solutions réelles à certaines équations. Cependant, elle permet également de résoudre des équations sans solution réelle. Ainsi, l’équation ![]() n’a pas de solution réelle, mais a deux solutions complexes :
n’a pas de solution réelle, mais a deux solutions complexes : ![]() et
et ![]() .
.













![Rendered by QuickLaTeX.com \[\renewcommand*{\arraystretch}{1.5} \begin{array}{rcl} \Delta \leqslant 0 &\Rightarrow& \left(2 \left\langle u , v \right\rangle\right)^2 + 4 \times \left\lVert u \right\rVert^2 \times \left\lVert v \right\rVert^2 \leqslant 0 \\ &\Rightarrow& 4 \left\langle u , v \right\rangle^2 - 4 \left\lVert u \right\rVert^2 \left\lVert v \right\rVert^2 \leqslant 0 \\ &\Rightarrow& \left\langle u , v \right\rangle^2 \leqslant \left\lVert u \right\rVert^2 \left\lVert v \right\rVert^2 \\ &\Rightarrow& \sqrt{\left\langle u , v \right\rangle^2} \leqslant \sqrt{\left\lVert u \right\rVert^2} \sqrt{\left\lVert v \right\rVert^2} \\ &\Rightarrow& \left| \left\langle u , v \right\rangle \right| \leqslant \left\lVert u \right\rVert \left\lVert v \right\rVert \\ \end{array}\]](https://coindesmaths.fr/wp-content/ql-cache/quicklatex.com-69489a27e6c51b06026267ac6f83974c_l3.png)
![Rendered by QuickLaTeX.com \[(a + b + c)^2 = \left( \sqrt{\frac{a}{x}} \sqrt{ax} + \sqrt{\frac{b}{x}} \sqrt{bx} + \sqrt{\frac{c}{x}} \sqrt{cx} \right)^2 \leqslant \left( \dfrac{a}{x} + \dfrac{b}{y} + \dfrac{c}{z} \right) \left( ax + by + cy \right)\]](https://coindesmaths.fr/wp-content/ql-cache/quicklatex.com-3c6832797e23951dbd06386f56c9e2b7_l3.png)
![Rendered by QuickLaTeX.com \[\renewcommand*{\arraystretch}{1.5} \left\lbrace\begin{array}{rcl} \sqrt{\frac{a}{x}} &=& \lambda \sqrt{ax} \\ \sqrt{\frac{b}{y}} &=& \lambda \sqrt{by} \\ \sqrt{\frac{c}{z}} &=& \lambda \sqrt{cz} \end{array}\right. \quad\Longleftrightarrow\quad \left\lbrace\begin{array}{rcl} \sqrt{a} &=& \lambda \sqrt{a}x \\ \sqrt{b} &=& \lambda \sqrt{b}y \\ \sqrt{c} &=& \lambda \sqrt{c}z \end{array}\right. \quad\Longleftrightarrow\quad \left\lbrace\begin{array}{rcl} \frac{1}{\lambda} &=& x \\ \frac{1}{\lambda} &=& y \\ \frac{1}{\lambda} &=& z \end{array}\right.\]](https://coindesmaths.fr/wp-content/ql-cache/quicklatex.com-a209c153f19cfe54118bb4ea7ed0c48d_l3.png)
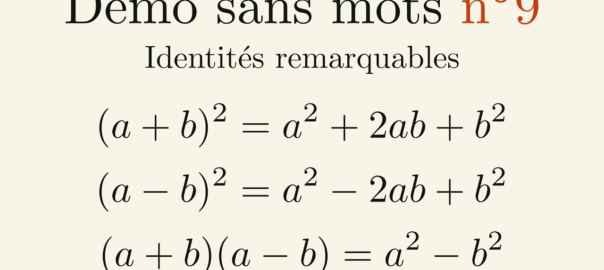
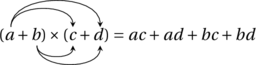
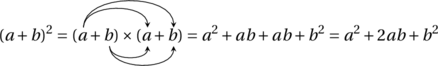
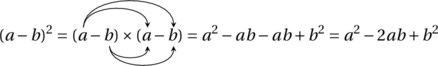
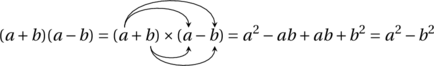

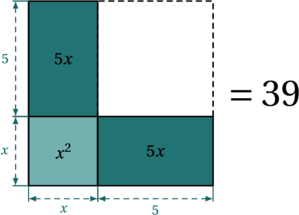
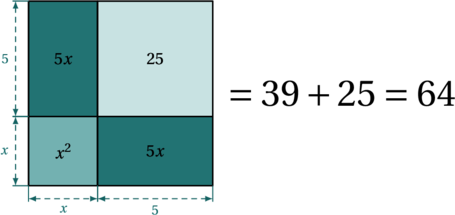

![Rendered by QuickLaTeX.com \[A = ab \leqslant \left( \frac{a + b}{2} \right)^2 = \left( \frac{\frac{P}{2}}{2} \right)^2 = \left( \frac{P}{4} \right)^2 = \frac{P^2}{16}\]](https://coindesmaths.fr/wp-content/ql-cache/quicklatex.com-4746efbfe56b372c4edcf7b0859cd42b_l3.png)