La vidéo : Théorème de Pythagore

Cette fois dans « Démo Sans Mots« , nous allons aborder le célèbre théorème de Pythagore.

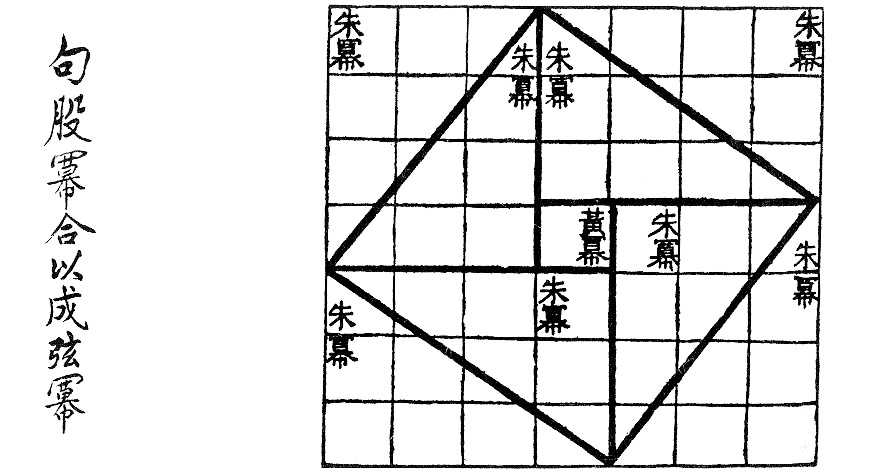
J’ai trouvé cette démonstration dans le livre Proof without words I de Roger B. Nelsen, à la page 1. Cependant, comme le dit l’auteur, cette preuve est elle-même adaptée du Zhoubi Suanjing, textes chinois écrits vers 200 avant J.-C.

Autour des racines carrées

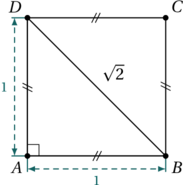
Dans la Grèce antique, les pythagoriciens croyaient que toutes les longueurs pouvaient être exprimées comme des fractions, c’est-à-dire comme rapports entre deux nombres entiers. Cependant, lorsqu’ils tentèrent de calculer la diagonale d’un carré de côté 1 en utilisant le théorème de Pythagore, ils firent une découverte surprenante : la longueur de cette diagonale est égale à la racine carrée de 2, un nombre irrationnel. Cette révélation choqua les mathématiciens pythagoriciens, remettant en question leur vision du monde où les nombres rationnels régnaient en maîtres. Depuis, les racines carrées irrationnelles ont été acceptées par l’ensemble des mathématiciens.

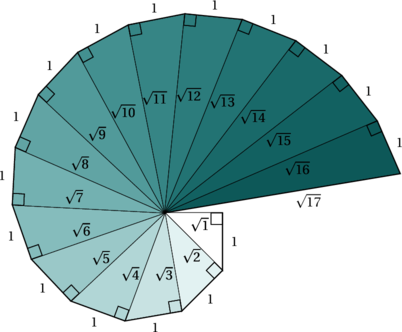
En 1941, un certain Jakob Heinrich Anderhub a eu l’idée de créer une sorte spirale en utilisant 16 triangles rectangles. Ces triangles permettent d’obtenir les racines des nombres de 2 à 17. Depuis lors, on appelle cette création la « spirale de Théodore », bien qu’on ne soit pas certain que Théodore de Cyrène ait utilisé cette méthode.

Histoire du théorème

Le théorème de Pythagore constitue l’une des pierres angulaires des mathématiques. En effet, on peut trouver des traces de ce théorème chez plusieurs civilisations, et ce bien avant les Grecs.

Babyloniens

Les Babyloniens, dès le 2^e millénaire avant notre ère, ont laissé des preuves de leur utilisation du théorème de Pythagore. Ils semblent avoir découvert une méthode afin de calculs de longueurs dans des triangles rectangles.

Sur la tablette Plimpton 322, datant d’environ 1800 avant J.-C., se trouve une liste de nombre. Les nombres des colonnes 2 et 3 font partie de triplets pythagoriciens. Par exemple, sur la ligne 11, on trouve les nombres 45 et 75. Or :

Ce triplet est donc complété par 60. Cela démontre ainsi une connaissance pratique des relations entre ces mesures dans un triangle rectangle.

Égypte

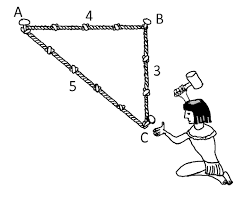
En Égypte ancienne, bien qu’il n’existe pas de preuve concrète du théorème de Pythagore, nous pouvons trouver des indices de la compréhension des triangles rectangles par les égyptiens. En effet, les géomètres arpenteurs égyptiens avaient l’habitude d’utiliser une corde à 13 nœuds pour délimiter les parcelles agricoles à chaque crue du Nil. Celle-ci permet de former un triangle dont les côtés ont pour longueurs 3, 4 et 5 nœuds, comme illustré ci-dessous. Selon la réciproque du théorème de Pythagore, ce triangle est rectangle car . Les arpenteurs pouvaient ainsi tracer des parcelles rectangulaires.

Chine

En Chine, le théorème de Pythagore, connu sous le théorème de Gougu (« gou » voulant dire « base » et « gu » signifiant « hauteur ») a également été exploré dans des textes anciens tels que le Zhoubi Suanjing (ou « Classique mathématique du Gnomon des Zhou »). Datant au plus tard d’environ 200 av. J.-C., ce texte chinois montre que les mathématiciens chinois avaient une compréhension avancée des propriétés des triangles rectangles. Bien que leur approche diffère de celle des Grecs, les Chinois ont également découvert des triplets pythagoriciens et ont appliqué leurs connaissances géométriques à divers domaines, y compris l’astronomie et l’ingénierie.

Son importance en mathématiques a fait du théorème de Pythagore le théorème ayant le plus de démonstrations, dont près de 370 sont recensées par Elisha Scott Loomis dans The Pythagorean Proposition. Ce dernier précise que le nombre de preuves est sans limite, et que les démonstrations n’utilisant que de la trigonométrie étaient impossibles. Or, le 18 mars 2023, Ne’Kiya Jackson et Calcea Johnson, deux étudiantes américaines, ont mis au point une telle démonstration. L’histoire de ce théorème n’est donc pas encore terminée.