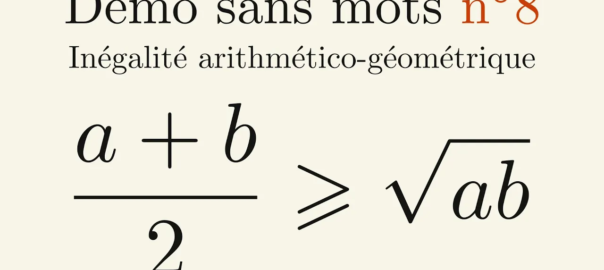Miniature de la vidéo numéro 8 de la série Démo Sans Mots, qui porte sur l'inégalité arithmético-géométriques.

Inégalité arithmético-géométrique – DSM#8

Mathématiques, Vidéos, ,

La vidéo : Inégalité arithmético-géométrique

Aujourd’hui dans « Démo sans mots« , nous allons nous intéresser à une inégalité bien pratique : l’inégalité arithmético-géométrique.

Cette démonstration provient du livre Proof without words de Roger B. Nelsen, à la page 51.

Y a moyen de moyenner

Dans la vie courante, quand on pense à calculer une moyenne, on pense souvent à ce qu’on appelle la moyenne arithmétique. C’est par exemple le cas dans l’éducation pour les moyennes trimestrielles. En réalité, il existe d’autres façons de calculer une moyenne, et c’est l’objet de cette section.

Moyenne arithmétique

C’est la moyenne la plus connue. Celle qu’on a l’habitude d’utiliser. La moyenne arithmétique des nombres a_1, \ldots, a_n \in \mathbb{R} est donnée par :

      \[m_a (a_1, ..., a_n) = \dfrac{a_1 + \ldots + a_n}{n}\]

Exemple : La moyenne arithmétique de 3, 8 et 10 est : \dfrac{3 + 8 + 10}{3} = 7.

Moyenne géométrique

Si la moyenne arithmétique consiste à additionner n nombres puis à diviser leur somme par n, la moyenne géométrique revient quant à elle à multiplier n nombres puis à prendre la racine n-ième du produit. La moyenne géométrique des nombres a_1, \ldots, a_n \in \mathbb{R}^+ est donnée par : 

      \[m_g (a_1, ..., a_n) = \sqrt[n]{a_1 \times \ldots \times a_n} = (a_1 \times \ldots \times a_n)^\frac{1}{n}\]

Exemple : La moyenne géométrique de 3, 8 et 10 est : \sqrt[3]{3 \times 8 \times 10} \approx 6,21.

Moyenne harmonique

Calculons maintenant la moyenne des inverses de n nombres, puis prenons son inverse. C’est comme ça qu’on obtient la moyenne harmonique. La moyenne harmonique des nombres a_1, \ldots, a_n \in \mathbb{R}^{+*} est donnée par :

      \[m_h (a_1, ..., a_n) = \dfrac{n}{\frac{1}{a_1} + \ldots + \frac{1}{a_n}}\]

Exemple : La moyenne harmonique de 3, 8 et 10 est : \dfrac{3}{\frac{1}{3} + \frac{1}{8} + \frac{1}{10}} \approx 5,37.

Moyenne quadratique

À la manière de la moyenne harmonique, calculons la moyenne des carrés de n nombres, puis prenons sa racine carrée. Nous obtenons alors la moyenne quadratique de ces nombres. La moyenne quadratique des nombres a_1, \ldots, a_n \in \mathbb{R}^+ est donnée par :

      \[m_q (a_1, ..., a_n) = \sqrt{\dfrac{a_1^2 + \ldots + a_n^2}{n}}\]

Exemple : La moyenne quadratique de 3, 8 et 10 est : \sqrt{\dfrac{3^2 + 8^2+ 10^2}{3}} \approx 7,59.

Remarque

Au fur et à mesure de nos exemples, nous avons pu observer les inégalités suivantes :

      \[\min(3,8,10) = m_h (3,8,10) \leqslant m_g (3,8,10) \leqslant m_a (3,8,10) \leqslant m_q (3,8,10) = \max(3,8,10)\]

En réalité, ces inégalités sont vraies peu importe les nombres dont on calcule ces moyennes. C’est en effet ce que la vidéo démontre pour les moyennes arithmétiques et géométriques de deux nombres.

De plus, toutes ces inégalités sont des égalités lorsque tous les nombres sont égaux.

Moyenne d’ordre p

Pour aller plus loin, je vais vous présenter la moyenne d’ordre p \in \mathbb{R} des nombres a_1, \ldots, a_n \in \mathbb{R} :

      \[M_p (a_1, \ldots, a_n) = \sqrt[p]{ \frac{1}{n} \sum_{k=1}^n a_k^p \right) }\]

Toutes les moyennes que nous avons vues précédemment peuvent s’écrire sous cette forme, ou comme limite de moyenne de cette forme.

Valeur de pNomExpression
p \to -\inftyMinimumM_{-\infty} (a_1, \ldots, a_n) = \min(a_1, \ldots, a_n)
p = -1Moyenne harmoniqueM_{-1} (a_1, \ldots, a_n) = \dfrac{n}{\frac{1}{a_1} + \ldots + \frac{1}{a_n}}
p \to 0Moyenne géométriqueM_0 (a_1, \ldots, a_n) = \sqrt[n]{a_1 \times \ldots \times a_n}
p = 1Moyenne arithmétiqueM_1 (a_1, \ldots, a_n) = \dfrac{a_1 + \ldots + a_n}{n}
p = 2Moyenne quadratiqueM_2 (a_1, \ldots, a_n) = \sqrt{\dfrac{a_1^2 + \ldots + a_n^2}{n}}
p \to +\inftyMaximumM_\infty (a_1, \ldots, a_n) = \max(a_1, \ldots, a_n)

On peut remarquer que ces moyennes se retrouvent dans le même ordre que dans l’inégalité.

Le plus grand enclos

Les inégalités que nous venons de voir peuvent être très utiles pour des problèmes d’optimisation. L’inégalité arithmético-géométrique nous sera par exemple utilise pour résoudre le problème suivant :

Problème : Un berger vient d’acheter 400m de clôture. Avec cette clôture, il veut créer un enclos rectangulaire. Cependant, il veut aussi que cet enclos soit le plus grand possible pour ses moutons. Quelle forme doit-il donner à son enclos ?

Nous cherchons donc un rectangle d’aire A maximale pour un périmètre P donné.

Notons a et b la longueur et la largeur d’un rectangle de périmètre P = 400. Son aire est donc A = ab et son périmètre est P = 2(a + b).

Rendered by QuickLaTeX.com

En utilisant l’inégalité arithmético-géométrique et le fait que a + b = \frac{P}{2}, on a :

      \[A = ab \leqslant \left( \frac{a + b}{2} \right)^2 = \left( \frac{\frac{P}{2}}{2} \right)^2 =  \left( \frac{P}{4} \right)^2 = \frac{P^2}{16}\]

En remplaçant P par 400, on a finalement que :

      \[A \leqslant \frac{400^2}{16} = \frac{160000}{16} = 10 000 = 100^2\]

Or, on a vu que cette inégalité est une égalité si et seulement si a = b. Donc l’aire maximale est atteinte lorsque a=b, c’est-à-dire pour un carré, d’aire 10000.

Notre berger doit donc construire un enclos carré de 100m de côté.

Laisser un commentaire