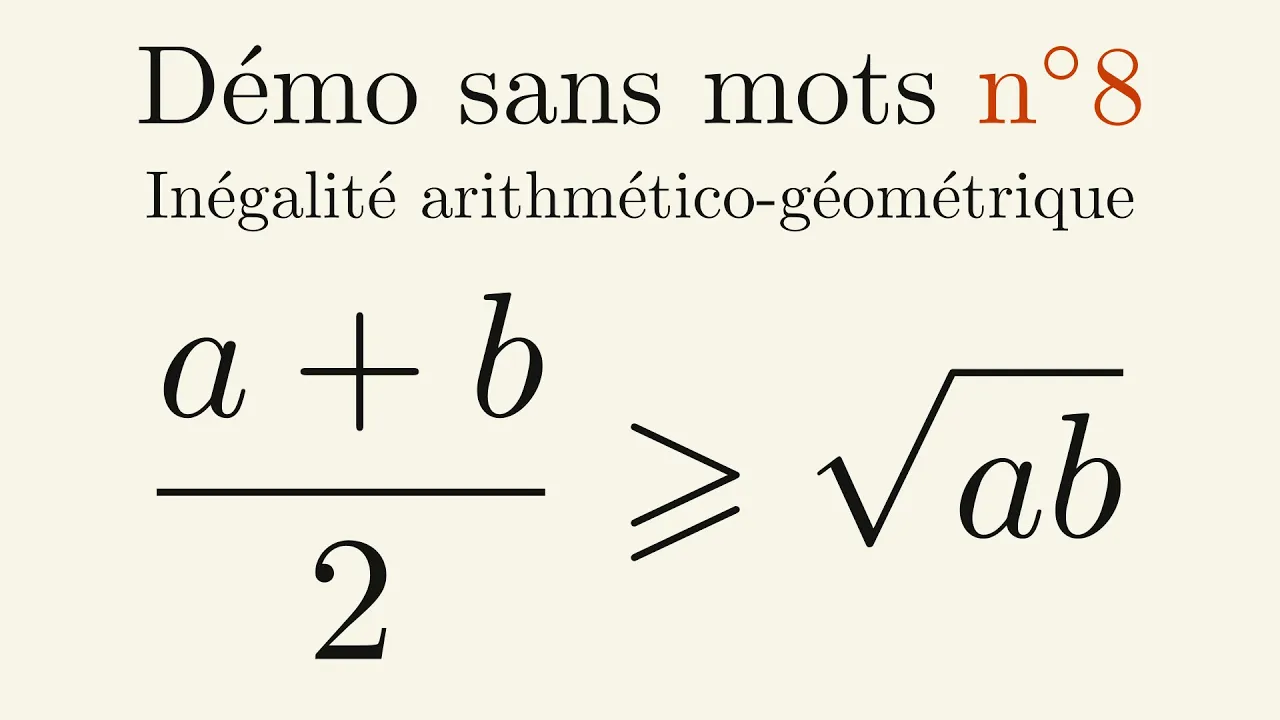Voici mon blog ! N’oubliez pas de vous abonner !
-
Démo sans mots
Aujourd’hui, j’ai le plaisir de vous annoncer le lancement d’une série de vidéos mathématiques passionnantes intitulée « Démo sans mots ». L’objectif est de rendre les concepts mathématiques plus accessibles et de mettre en avant la beauté des mathématiques.
-
Pixel art pédagogique
Si vous avez des élèves qui préfèrent dessiner plutôt que de faire des mathématiques, l’outil que je vais vous présenter pourrait vous être utile. En effet, l’outil que je vais vous présenter est un générateur de pixel art.
-
Calendrier scolaire perpétuel
Chaque année a son calendrier, ses jours fériés et ses vacances scolaires. Voici donc un calendrier scolaire perpétuel, qui se remplit automatiquement une fois l’année choisie.
-
Mes graphiques Desmos
Desmos est une calculatrice graphique en ligne disponible gratuitement en version navigateur et en version application mobile. Voici une sélection de graphique de ma création. Ils sont évidemment utilisables et partageables.
-
Histoire des nombres complexes
Les nombres complexes sont apparus afins de résoudre certains problèmes. L’essor des mathématiques pendant la renaissance italienne a amené à résoudre de tels problèmes, et leur méthode de résolution donnera par la suite les nombres complexes qu’on connait aujourd’hui. Dans cet article, nous allons voir en détail l’histoire de leur apparition.
-
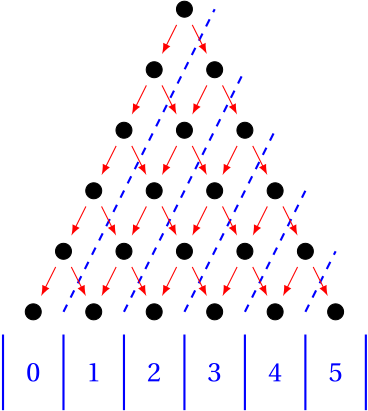
Planche de Galton
Francis Galton, scientifique britannique pionnier des statistiques, a conçu la planche de Galton, un dispositif où des billes dévalent des rangées de clous, dévient aléatoirement. Nous allons calculer la probabilité qu’une bille finisse sa course dans un compartiment spécifique.
-
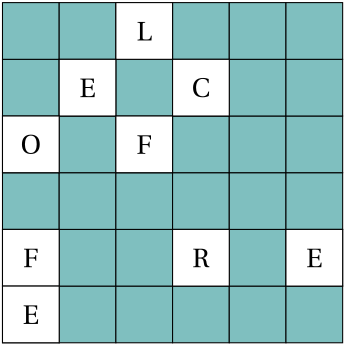
Grille tournante de Fleissner
Histoire de la grille de Fleissner La méthode des grilles tournantes, popularisée par le colonel autrichien Fleissner dans son ouvrage « Handbuch der Kryptographie », a marqué l’histoire de la cryptographie. L’armée allemande a largement utilisé cette méthode pendant la Première Guerre mondiale, à partir de la fin de l’année 1916. Chaque grille avait un nom de…
-
Inégalité de Cauchy-Schwarz – DSM#10
Cet épisode explore l’inégalité de Cauchy-Schwarz, montrant son application dans le calcul d’aires de parallélogrammes et la minimisation d’une expression liée aux côtés d’un triangle. Une démonstration élégante est présentée, mettant en lumière la pertinence de cette inégalité dans divers contextes mathématiques.
-
Identités remarquables – DSM#9
Cette fois dans « Démo sans mots » présente les identités remarquables et les étapes pour les démontrer, ainsi que la méthode géométrique d’Al-Khwarizmi pour résoudre les équations quadratiques.
-
Inégalité arithmético-géométrique – DSM#8
Découvrez les moyennes mathématiques et l’inégalité arithmético-géométrique, ainsi que leur application pour optimiser l’aire d’un enclos rectangulaire de périmètre donné.
Abonnez-vous à mon blog
Recevez directement le nouveau contenu dans votre boîte de réception.