La vidéo : Théorème de Viviani

Aujourd’hui dans « Démo Sans Mots« , nous allons voir un théorème que je trouve très élégant et trop peu connu. Il s’agit du théorème de Viviani.

Cette démonstration vient du livre Proof without words III de Roger B. Nelsen, à la page 21.

Une démonstration algébrique

Pour une autre démonstration de ce joli théorème, nous allons utiliser la figure suivante, où le triangle est équilatéral.

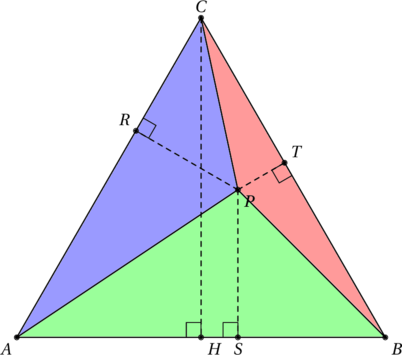
Il ne reste maintenant qu’une chose à remarquer. L’aire du triangle est tout simplement la somme des aires des triangles , et .

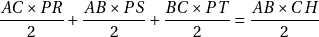
Puisque le triangle est équilatéral, on peut remplacer et par dans cette expression.

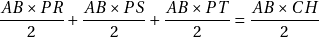
En simplifiant chaque membre de cette égalité par , on obtient finalement que . C’est bien le résultat attendu.

Diagrammes ternaires

Les diagrammes ternaires sont des outils visuels utilisés notamment en chimie et en science des matériaux. En effet, ils permettent de représenter la composition et les proportions relatives de trois composants dans un système. Il s’agit en fait d’un triangle équilatéral dont chaque sommet représente un composant. Des lignes à l’intérieur du triangle peuvent délimiter différentes phases ou régions de compositions possibles.

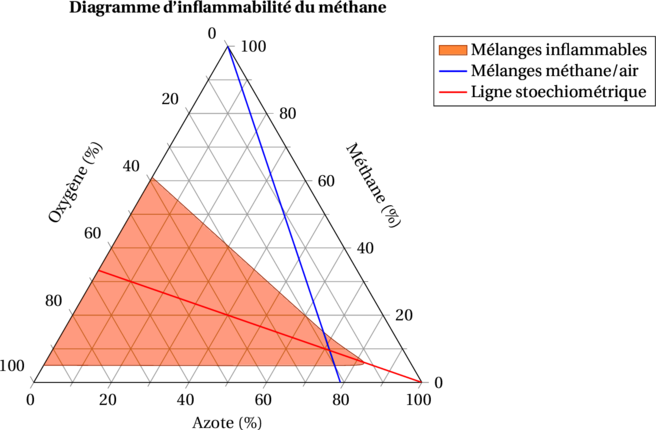
Les diagrammes ternaires sont essentiels pour comprendre les mélanges complexes et les équilibres de phases. Ils permettent par exemple aux chercheurs d’analyser et de prédire les comportements des systèmes à plusieurs composants de manière concise et visuelle.