Présentation générale
Francis Galton (1822-1911), issu d’une famille de scientifiques et cousin de Charles Darwin, s’est intéressé à l’hérédité des capacités intellectuelles pour améliorer l’espèce humaine. Son expertise couvrait la géographie, la météorologie et l’anthropologie en plus de ses contributions pionnières aux statistiques à des fins pratiques.
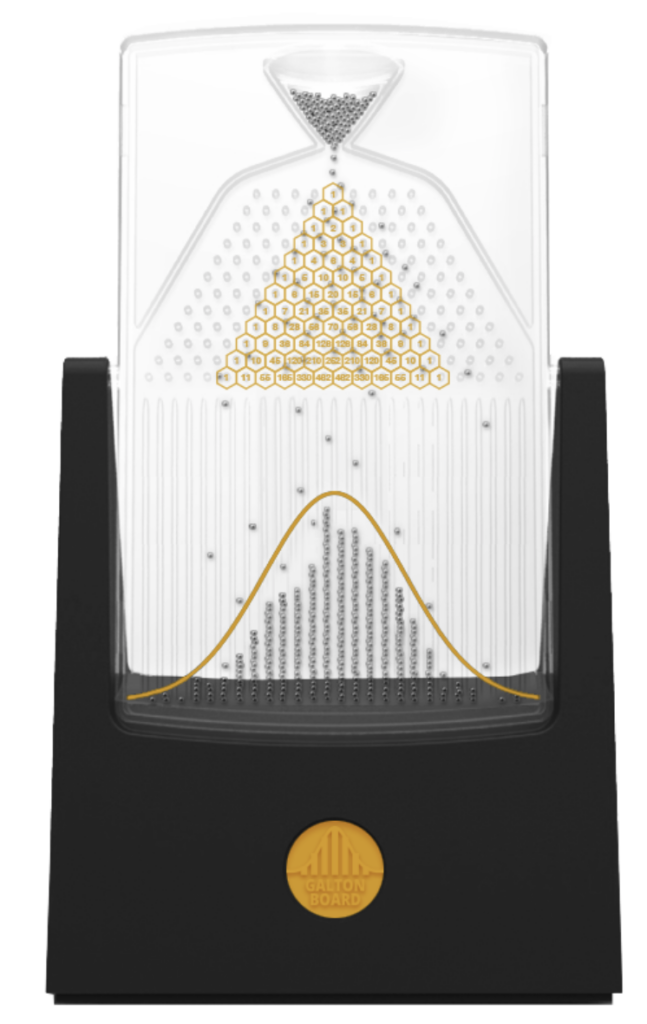
La planche de Galton, aussi appelée « Quincunx » ou « machine de Galton », est un dispositif conçu par Francis Galton. Elle comporte une série de clous disposés en quinconce, au travers desquels tombent des billes déviant aléatoirement à gauche ou à droite. En bas, les billes s’accumulent dans des compartiments.
Chaque compartiment a-t-il la même chance de recevoir la bille ?
Essayons de calculer la probabilité qu’un compartiment donné reçoive une bille. Supposons que la planche de Galton présente ![]() rangées de clous.
rangées de clous.
Chaque fois qu’une bille tape un clou, elle a une chance sur deux de tomber à sa gauche et une chance sur deux de tomber à sa droite. Ainsi, chaque changement de direction a autant de chance de se produire, et toutes les trajectoires possibles sont équiprobables. La probabilité que la bille finisse sa course dans un compartiment donné est donc :
![Rendered by QuickLaTeX.com \[p = \frac{\text{Nombre de trajectoires allant dans le compartiment}}{\text{Nombre de trajectoires au total}}\]](https://coindesmaths.fr/wp-content/ql-cache/quicklatex.com-76c73bb7a17caa6b8da24ce2e0eb5760_l3.png)
Il nous faut donc dénombrer le nombre de trajectoire au total ainsi que le nombre de trajectoires allant dans un compartiment spécifique.
Calcul du dénominateur
Commençons par le dénominateur. Chaque clou crée une bifurcation dans la trajectoire de la bille. Cela permet alors de doubler le nombre de trajectoires possibles. Il y en a donc 2 après la première rangée de clous, 4 après la seconde, puis 8, puis 16… Après ![]() rangées, il y en a donc
rangées, il y en a donc ![]() trajectoires possibles au total.
trajectoires possibles au total.


Calcul du numérateur
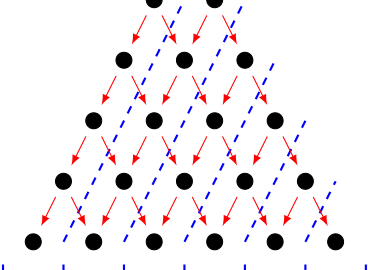
Passons au numérateur. On cherche maintenant à compter le nombre de chemins permettant à une bille d’aller dans un compartiment donné. Cela revient en réalité à compter le nombre de fois que cette bille doit rebondir à la droite d’un clou. En effet, cela peut être mis en avant grâce au schéma ci-contre.
À chaque fois qu’une bille tombe à la droite d’un clou, elle franchit l’une des lignes en pointillés bleus sans pouvoir revenir en arrière. Cela permet ainsi de compter le nombre de fois qu’elle rebondit à droite. Par exemple, pour aller dans le compartiment n°2, elle doit aller 2 fois à droite.
Ainsi, pour atteindre la ![]() -ième compartiment en partant de la gauche, la bille doit rebondir
-ième compartiment en partant de la gauche, la bille doit rebondir ![]() fois à droite parmi les
fois à droite parmi les ![]() rebonds au total. Or, c’est exactement la définition des coefficients binomiaux
rebonds au total. Or, c’est exactement la définition des coefficients binomiaux ![]() . Il y a donc
. Il y a donc ![]() chemins permettant à une bille de se retrouver dans le
chemins permettant à une bille de se retrouver dans le ![]() -ième compartiment après
-ième compartiment après ![]() rangées de clous.
rangées de clous.
Conclusion
Finalement, la probabilité que la bille finisse sa course dans le ![]() -ième compartiment après
-ième compartiment après ![]() rangées de clous est :
rangées de clous est :
![Rendered by QuickLaTeX.com \[\displaystyle p = \frac{1}{2^n} \binom{n}{k} = \frac{n!}{2^n k! (n-k)!}\]](https://coindesmaths.fr/wp-content/ql-cache/quicklatex.com-869ba0be0989f54adddb039b7df19edb_l3.png)
Voici les différentes valeurs de ![]() que l’on obtient pour
que l’on obtient pour ![]() allant de 0 à 5 et pour toutes les valeurs de
allant de 0 à 5 et pour toutes les valeurs de ![]() correspondantes :
correspondantes :
Animation
Ci-dessous une animation de la planche de Galton réalisée avec Desmos. Le curseur permet de contrôler la vitesse de l’animation. Une version plus complète est disponible ici.