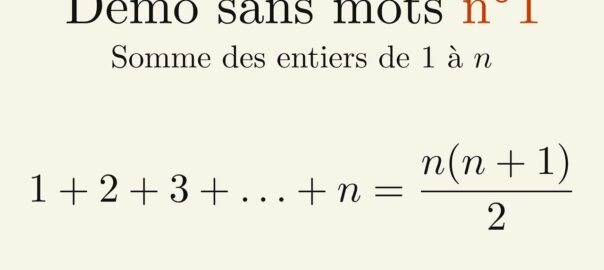La vidéo : Somme des entiers

Pour ce premier épisode de « Démo sans mots« , je vous propose une démonstration assez classique. En effet, nous allons parler de la somme des entiers de 1 à .

Cette démonstration provient du livre Proof without words de Roger B. Nelsen, à la page 69.

Je tiens tout de même à préciser que ceci n’est en réalité pas une démonstration du cas général, mais simplement l’exemple du cas . Mais bien sûr tous les autres cas fonctionnent de la même manière.

Une autre démonstration

Si on veut une démonstration algébrique de cette propriété, on peut s’inspirer de celle de Gauss. En effet, notre ami a fait preuve de brillance dès son jeune âge grâce à elle.

Selon la légende, lorsqu’il était à l’école primaire, il a été sanctionné par son enseignant pour mauvaise conduite. On lui a alors donné comme exercice d’additionner les nombres de 1 à 100. Étonnamment, il a réussi à calculer rapidement cette somme, qui s’élève à 5050.

Pour faire cette démonstration, je vais commencer par écrire la somme des entiers, notée , dans un sens et dans l’autre :

Cela nous permet de regrouper les termes deux par deux. Grâce à ce jeu d’écriture, chaque terme se retrouve en face d’un autre. De plus, chaque paire de termes a pour somme . En additionnant ces deux lignes, on peut donc en déduire que , puis que . On retrouve alors bien la formule attendue.

On peut noter que ces deux démonstrations ne font en réalité qu’une. En effet, l’escalier retourné dans la vidéo correspond exactement la somme écrite en sens inverse ci-dessus.

Nombres triangulaires

Avec la représentation utilisée dans la vidéo, le lien entre la somme des entiers et les nombres triangulaires est naturel. Ainsi, nous avons trouvé une expression explicite du -ième nombre triangulaire.

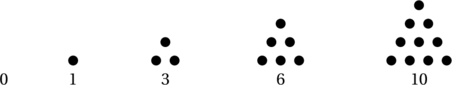
De la même manière, on peut démontrer par exemple que deux nombres triangulaires successifs donnent un nombre carré si on les additionne. Beaucoup d’autres démonstrations de ce type existent, et feront peut-être l’objet de futures vidéos.

Aujourd’hui, j’ai le plaisir de vous annoncer le lancement d’une série de vidéos mathématiques passionnantes intitulée « Démo sans mots« . L’objectif est de rendre les concepts mathématiques plus accessibles et de mettre en avant la beauté des mathématiques. Dans cette série, nous explorerons ainsi des théorèmes et des propriétés mathématiques en utilisant uniquement des démonstrations visuelles, sans aucun mot.

Que vous soyez étudiant, enseignant, ou simplement curieux, ces vidéos sont faites pour être accessibles au plus grand nombre. Pas besoin d’être un expert en mathématiques pour apprécier ces vidéos. Ainsi, vous trouverez dans « Démo sans mots » des démonstrations de résultats divers, tels que le théorème de Pythagore ou que l’inégalité de Cauchy-Schwarz.

Vous pourrez retrouver ces vidéos sur ma chaîne YouTube. Actuellement, j’ai déjà préparé dix épisodes. D’autres vidéos sont également en préparation et sortiront par la suite. Une vidéo sortira toutes les deux semaines, les mercredis à 16 heures.

Mais ce n’est pas tout ! En complément de chaque vidéo, je publierai un article détaillé sur ce blog. Dans ces articles, vous trouverez des explications approfondies sur les démonstrations visuelles présentées dans les vidéos. Vous aurez ainsi la possibilité d’approfondir le sujet et d’explorer des pistes intéressantes et non abordées.

J’ai hâte de commencer cette aventure et de partager ma passion pour les mathématiques à travers ces démonstrations visuelles. J’espère que cette série de vidéos inspirera et émerveillera les esprits curieux, tout en contribuant à démystifier les mathématiques.

N’oubliez pas de vous abonner à ma chaîne YouTube afin de ne manquer aucun épisode de « Démo sans mots ». Le lancement de la première vidéo est prévu pour le mercredi 9 août à 16 heures. Elle portera sur la somme des entiers de 1 à . N’hésitez pas à partager ces vidéos avec vos amis, vos collègues et toutes les personnes intéressées par les mathématiques.