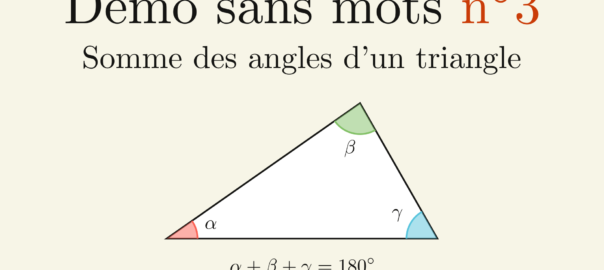
La vidéo : Somme des angles d’un triangle

Dans ce nouvel épisode de “Démo Sans Mots“, nous allons nous intéresser à la somme des angles d’un triangle.

Cette démonstration est inspirée de celle présente dans les Éléments d’Euclide (Livre I, Proposition XXXII).

Plus de précisions

Cette propriété des triangles bien connue des collégiens repose sur deux propriétés vues en cinquième : les angles correspondants et les angles opposés par le sommet. En effet, ces propriétés sont représentées par le glissement des angles et des segments. Notons de plus que ces deux propriétés sont également démontrées par Euclide dans ses Éléments, respectivement en tant que Propositions XV et XXIX.

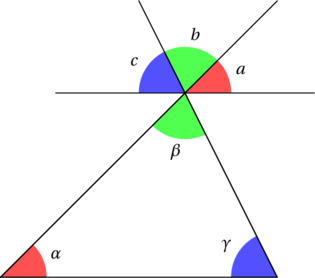
Dans la figure ci-dessus, les deux droites horizontales sont parallèles entre elles.

Commençons par montrer que les angles rouges et bleus sont les mêmes. On remarque en effet que les droites horizontales sont parallèles et que ces angles sont correspondants. On peut ainsi en déduire la relation . De la même manière, il vient que .

Pour les angles verts maintenant, il suffit de constater que ces angles sont opposés par le sommet. On a donc cette fois la relation .

Enfin, remarquons que nos trois angles , et forment bien un angle plat. On a donc finalement que .

En fait, c’est (parfois) faux

Il y aurait un problème dans notre raisonnement ? Eh bien non ! Notre raisonnement est bon. Néanmoins, dans notre démonstration, nous avons fait une hypothèse à la fois simple et très forte : nous avons utilisé la géométrie euclidienne. Cela signifie tout simplement que nous avons considéré des triangles dans le plan.

En effet, si on regarde des triangles ailleurs que dans un plan, on peut trouver des triangles dont la somme des angles est supérieure à 180°. Si on se place sur une sphère, on peut même trouver des triangles avec trois angles droits, comme dans l’illustration ci-dessous.

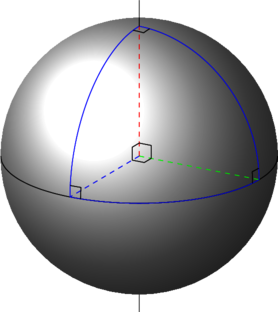
On peut également trouver des triangles dont la somme des angles est inférieure à 180° en géométrie hyperbolique.

Bref, il faut toujours faire attention à ce que l’on sait avec d’en tirer des conclusions.