Histoire de la grille de Fleissner

La méthode des grilles tournantes, popularisée par le colonel autrichien Fleissner dans son ouvrage « Handbuch der Kryptographie », a marqué l’histoire de la cryptographie. L’armée allemande a largement utilisé cette méthode pendant la Première Guerre mondiale, à partir de la fin de l’année 1916. Chaque grille avait un nom de code spécifique : « Anna » pour la grille , « Berta » pour la grille , « Clara » pour la grille , « Dora » pour la grille , « Emil » pour la grille et « Franz » pour la grille .

L’attribution de l’invention de cette méthode à Fleissner reste sujette à débat. Bien que des techniques de chiffrement par grille existent depuis longtemps, le nom de Fleissner est étroitement associé à cette méthode, en partie grâce à Jules Verne. En effet, dans son roman « Mathias Sandorf » publié en 1885, Verne fait référence à cette technique de cryptographie et l’attribue à Fleissner, contribuant ainsi à consolider son lien avec cette méthode dans l’imaginaire collectif.

Fonctionnement de la grille de Fleissner

Codage

Pour coder un message à l’aide d’une grille Fleissner, on commence par inscrire les lettres dans les espaces vides de la grille. Une fois la grille remplie, on la fait pivoter d’un quart de tour vers la droite, puis on continue à remplir les cases vides avec les lettres du message. On répète ensuite ce processus jusqu’à remplir toutes les 36 cases de la grille.

Cependant, si le message est plus court que le nombre total de cases à remplir, on complète avec des lettres quelconques pour remplir la grille.

Codons par exemple le message suivant : « Le coffre est enterré au pied d’un arbre ». Les deux premières étapes donnent :

Les deux étapes suivantes donnent :

Finalement, le message codé se présente sous la forme du tableau de lettres suivant :

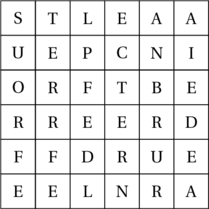
Décodage

Pour décoder un message codé grâce à une grille de Fleissner, il suffit de réaliser l’opération inverse. En tournant la grille d’un quart de tour, nous pouvons noter les lettres qui apparaissent sur une feuille blanche.

Bien évidemment, il est nécessaire d’avoir la grille ayant servi au codage pour pouvoir décoder le message. Des méthodes pour retrouver la grille existent (comme ici), mais peuvent ne pas s’avérer concluantes.

Création d’une grille de Fleissner

Pour créer une grille de Fleissner, il faut choisir quels trous percer. Nous allons nous limiter dans un premier temps aux grilles de taille 6 pour simplifier le raisonnement.

Sur une grille de Fleissner, un même trou montrera 4 lettres différentes au fur et à mesure des rotations. Ainsi, si la case du coin supérieur gauche de la grille est trouée, elle dévoilera les lettres placées aux quatre coins. De la même manière, toutes les cases du coin supérieur gauche dévoileront en tout quatre lettres. Chaque lettre étant dans un quart différent de la grille.

Nous pouvons donc numéroter comme ci-dessous chaque case de la grille avec un numéro allant de 1 à 9. Deux cases auront le même numéro si elles sont dévoilées par le même trou. Pour créer une grille de Fleissner, il faut donc trouer chaque numéro de 1 à 9 une seule fois.

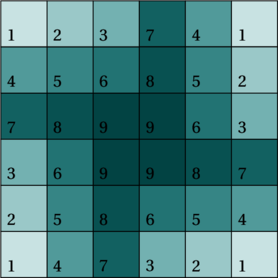
Cette numérotation des cases permet également de facilement calculer le nombre de grilles distinctes possibles. En effet, chacun des 9 trous peut prendre 4 positions différentes. Il y a grille de taille 6 possibles.

On peut même pousser ce même raisonnement pour créer des grilles de taille ainsi que pour montrer qu’il en existe .