A - Modélisation par un graphe
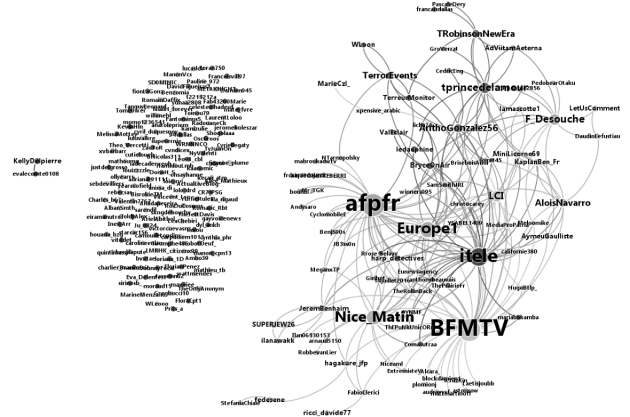
On peut représenter un réseau social par un graphe, un objet mathématique permettant de modéliser des relations. Dans ce graphe, les sommets correspondent aux personnes inscrites sur le réseau social, et les arêtes représentent les relations entre ces personnes. Chaque sommet symbolise donc un individu, et chaque lien indique l’existence d’une relation sociale.
Exemple :
Les relations entre différents individus ayant créé leur profil sur un réseau social peuvent ainsi être représentées sous la forme d’un graphe. Le lien entre deux personnes indique qu’ils sont « amis » sur ce réseau.
Par exemple, dans le graphe étudié, Jean est ami avec Yasmine, mais il n’est pas ami avec Arnaud, ce qui se traduit par la présence ou l’absence d’un lien entre les sommets correspondants.
Les réseaux sociaux peuvent donc être représentés sous la forme de graphes mathématiques. Ces graphes possèdent plusieurs caractéristiques importantes qui permettent de les analyser et de mieux comprendre leur structure :
Distance entre deux sommets : nombre minimal d’arêtes à parcourir pour aller d’un sommet à un autre. Elle indique à quel point deux personnes sont proches dans le réseau.
Écartement d’un sommet : distance maximale entre ce sommet et tous les autres sommets du graphe. Il mesure l’éloignement le plus important depuis une personne donnée.
Diamètre d’un graphe : distance maximale entre deux sommets du graphe. Il donne une idée de la taille du réseau en termes de connexions.
Centre d’un graphe : sommet dont l’écartement est minimal. Il correspond à une position stratégique dans le réseau.
Rayon d’un graphe : valeur de l’écartement depuis son centre. Il représente la distance maximale entre le centre et les autres sommets.
Exemple :
Graphe
Une représentation graphique qui facilite la compréhension des connexions et des relations au sein d’un ensemble.
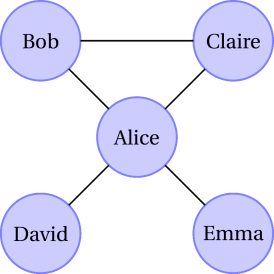
Matrice d’adjacence
Une représentation informatique d’un graphe consiste souvent à utiliser une matrice d’adjacence. Il s’agit d’un tableau à deux dimensions qui indique, pour chaque paire de sommets, s’ils sont reliés ou non. Cette forme est particulièrement adaptée au traitement des graphes par un ordinateur.
Alice | Bob | Claire | Emma | David | |
|---|---|---|---|---|---|
Alice | 0 | 1 | 1 | 1 | 1 |
Bob | 1 | 0 | 1 | 0 | 0 |
Claire | 1 | 1 | 0 | 0 | 0 |
Emma | 1 | 0 | 0 | 0 | 1 |
David | 1 | 0 | 0 | 1 | 0 |
Pour ce graphe, on a :
Sommet | Alice | Bob | Claire | Emma | David |
|---|---|---|---|---|---|
Écartement | 1 | 2 | 2 | 2 | 2 |
Le diamètre de ce graphe est égal à 2, ce qui correspond à l’écartement maximal. Son centre est Alice, car c’est le sommet dont l’écartement est minimal. Son rayon est égal à 1, car c’est l’écartement du centre.
Ces graphes permettent par exemple de déterminer la popularité d’un individu et d’identifier les influenceurs au sein d’un réseau social.
Les nœuds centraux, qui possèdent un degré de connexion élevé, correspondent souvent à des profils influents capables de diffuser l’information plus rapidement. L’analyse des graphes permet ainsi de comprendre comment circule le contenu partagé, et comment certaines informations peuvent se propager très vite, du biais cognitif à la fake news, comme le souligne Mehdi Moussaïd ci-dessous.